Нецентрированный коэффициент детерминации регрессионной модели.
Коэффициент детерминации показывает долю дисперсии результативного признака x, объясняемую регрессией, в общей дисперсии y. Иными словами, долю влияния фактора на изменение результативного показателя.
Например, коэффициент детерминации равен 0,78. Это значит, что изменения результативного показателя на 78% объясняются изменениями уравнения регрессии или модель среднего качества.
Коэффициентом детерминации называется статистика, определяемая по формуле (справедливо только в случае включения свободный член):
,R-2.=1-,ESS-TSS.=1-,,e-T.e-,y-T.y.=,RSS-TSS.=,,,y.-T.,y.-,y-T.y., 0≤,R-2.≤1 (1)
где:
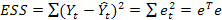 – необъясненная регрессией (остаточная) сумма квадратов отклонений (error sum of squares);
– необъясненная регрессией (остаточная) сумма квадратов отклонений (error sum of squares);
 =
= 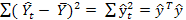 ‑ объясненная регрессией сумма квадратов отклонений (regression sum of squares);
‑ объясненная регрессией сумма квадратов отклонений (regression sum of squares);
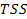 =
= 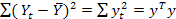 ‑ общая сумма квадратов отклонений зависимой переменной от ее среднего выборочного значения (total sum of squares).
‑ общая сумма квадратов отклонений зависимой переменной от ее среднего выборочного значения (total sum of squares).
Из формулы (1) следуют два масштабирующих значения для коэффициента детерминации:
•,R-2.=0, при RSS=,--,(,,Y.-t.-,Y.)-2.=0. в этом случае регрессор X не улучшает качество оценки (прогноза) 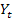 , по сравнению с обычной оценкой (прогнозом)
, по сравнению с обычной оценкой (прогнозом) 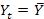 ;
;
• ,R-2.=1, при ,R-2.=1, в этом случае все точки наблюдения лежат на регрессионной прямой (т. е. 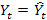 , или ,e-t.=0).
, или ,e-t.=0).
Таким образом, чем ближе значение коэффициента детерминации к 1, тем лучше качество подгонки (аппроксимация облака наблюдений линейной функцией) и оценка 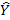 более точно аппроксимирует наблюдения
более точно аппроксимирует наблюдения 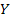 .
.
Дата добавления: 2015-01-10; просмотров: 3578;
