Оценка параметров парной регрессионной модели методом наименьших квадратов (МНК) в координатной форме.

Подставим вектор оценок параметров модели ( 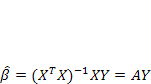) в выражение оценки эндогенной переменной ( 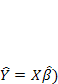, получим:

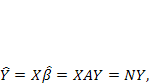
где

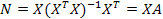
матрица линейного преобразования, матричный оператор, называемый проектором, в силу свойства идемпотентности (матрица N совпадает со своим квадратом: ):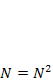

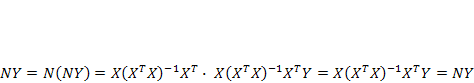
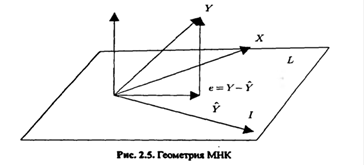
Таким образом, элементы вектора оценок являются проекцией вектора наблюдений У на плоскость L, проходящую через векторы, яв­ляющиеся столбцами расширенной матрицы регрессоров: I =(l,...,l)^T

и X. Вектор остатков е = У - , в соответствии с методом наименьших квадратов, должен иметь наименьшую длину, так как критерий отбора (функционал качества) МНК, в матричной форме, есть не что иное, как квадрат нормы вектора остатков

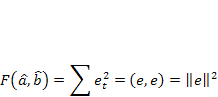
длина элемента евклидова пространства.

Длина будет наименьшей, если вектор е ортогонален плоскости L, т. с. ортогонален каждому вектору, принадлежащему данной плоскости, в частности, векторам / и X, а это означает, что скалярные произведения соответствующих векторов должны быть равны нулю, т. е.

Таким образом, мы снова получили необходимые условия экстре­мума — систему нормальных уравнений, в результате решения которой получаются МНК-оценки параметров модели, обеспечивающие мини­мальное значение функционалу качества.