Предпосылки Гаусса-Маркова относительно случайного возмущения регрессионной модели.

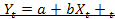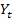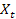Уравнения для отдельных наблюдений зависимой переменной Y записываются в виде (схема Гаусса-Маркова): , где , , t=1,…,n – выборочные данные (наблюдения), n –объем выборки (количество наблюдений)

Относительно возмущений Ԑt, t=1,..n, в регрессионных моделях принимаются следующие предположения (условия Гаусса-Маркова):

1) Математическое ожидание случайных возмущений равно нулю

E(Ԑt)=0, t=1,..n

2) Дисперсия возмущений постоянна и не зависит от номера (момента) наблюдений t

Var(Ԑt)=const=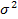

Независимость дисперсии возмущения от номера наблюдения называется гомоскедантичностью – одинаковый разброс. При нарушении – гетероскендантичность.

3) Возмущения для различных наблюдений некоррелированы:

Cov (Ԑt, Ԑs)=0 при t 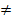s

Т.е. предполагается отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях tи s. При нарушении – автокорреляция возмущений.

4) Ковариация между регрессором и случайным возмущением равна 0. При парной регрессии можно не проверять.

Cov(Xt,Ԑt)=0