Расчет на прочность статически определимых стержней при изгибе

В разделе 1 была определена цель расчетов на прочность, проверка выполняет условие предельного состояния (поверочный расчет) или определение некоторых расчетов марки материала и т.д. из условия предельного состояние. Средством этого расчета является сопоставление небольшого по объему стержня с одним из критериев предельного состояния.

Для случая плоского поперечного изгиба, волокна параллельны оси стержня находится в состоянии одноосного растяжения / сжатия следовательно предельное состояние определяется условием при одноосном растяжении.

(*)

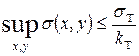Данный критерий соответствует отсутствию пластических деформаций в точке с наибольшем нормальным напряжением.

Рассмотрим распределение нормальных напряжений по высоте сечения. Принятые гипотезы приводят к выражению:

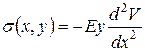
Вводя внутренний силовой фактор – изгибающий момент, мы связывали его с напряжением формулой:

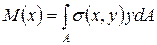
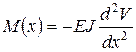
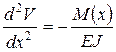(2.29)

Умножаем правую и левую части на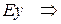

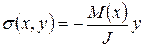(2.30)

(2.30) определяет распределение напряжений по высоте поперечного сечения через изгибающий момент.

В литературе по СопрМату знак в формуле (2.30) опускается; вычисляется абсолютная величина напряжения по абсолютной величине момента, а знак напряжения определяется в зависимости от расположения точки с координатой у в зоне растянутых / сжатых волокон.

у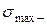

-

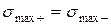
z h

+

b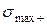

-

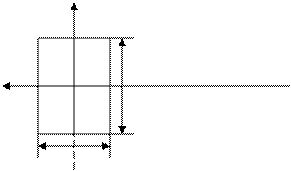
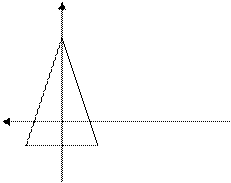
Сечение имеет осью симметрии одну из главных осей инерции.

у

-

z

+

Распределение напряжений по высоте поперечных сечений с 1 и 2 осями симметрии.

Вывод: Наибольшее по абсолютной величине напряжение возникает в точке поперечного сечения наиболее удаленной от центра тяжести в направлении той главной оси инерции, которая определяет плоскость изгиба. Исходя из цели расчета на прочность (*) эту формулу переписывают в следующем виде:

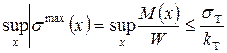(2.31)

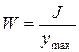(2.32)

(2.32) – момент сопротивления поперечного сечения.

(2.31) применяется в том случае, когда материал стержня имеет одинаковые одинаковые пределы текучести или прочности при растяжении и сжатии, т.е. эта формула справедлива для большинства металлов, однородных полимеров, хаотически напряженных композитов.

Если экспериментально установлено, что 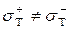, то вместо (2.31) используем условие предельного состояния при растяжении и сжатии по отдельности.

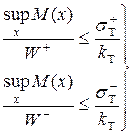(2.33)

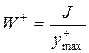
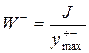(2.34)

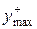и 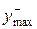- Координаты наиболее удобных точек в зонах растяжения и сжатия.