Кинематика деформирования при растяжении/сжатии

Рассмотрим волокно MN, которое в начальном состоянии имело длину dx. Относительная деформация этого волокна равна:

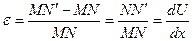(2.1)

Из рисунка следует, что все волокна параллельные оси получают одинаковые деформации. Если пренебречь изменением поперечных размеров и предположить, что волокна параллельны оси стержня не надавливают друг на друга, то любой из волокон параллелен оси стержня находится в состоянии одноосного растяжения (сжатия) и, следовательно, для вычисления напряжений можно принять закон Гука.

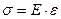(2.2)

Из (2.1) и (2.2) следует напряжение поперечного сечения при одноосном растяжении (сжатии) равномерно распределено по поперечному сечению.

В связи с тем, что распределение напряжение равномерно, удобно ввести их интегральную характеристику – продольную силу.

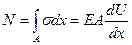(2.3)

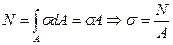(2.4)

Из последней формулы следует, что если удается построить зависимость от координаты х, то зная площадь поперечного сечения стержня можно построить эпюру напряжений в стержне.

Рассмотрим, равновесие участка стержня длиной dx рассматривая только продольную силу.

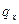- распределенная внешняя нагрузка.

Будем считать, что dx – бесконечно малая величина, так что нагрузку 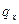можно считать постоянной.

Составим уравнения проекций всех сил ось стержня.

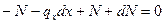
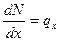(2.5)

Если подставить в последнюю формулу, формулу (2.3), то получим дифференциальное уравнение стержня в перемещениях.

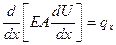(2.6)

Предполагается, что жесткость стержня на растяжении ЕА может быть гладкой и непрерывной функцией координаты х. (2.6) нетрудно проинтегрировать:

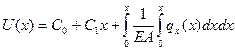(2.7)

Предположим, что на стержне определено начало координат. Например, на левом конце и ось х направлена с лева на право. Если подставить в (2.7) х=0, то

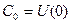
Если продифференцировать это выражение, получим

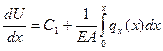
Умножая последнее выражение на ЕА, получим:

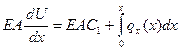
Записывая это выражение для начала участка:

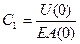
Таким образом, общее решение уравнения в перемещениях имеет вид:

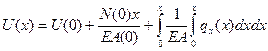(2. 8)

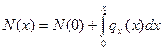(2.9)

При решении (2.9) мы можем удовлетворить только одну краевому условию. Если закрепление стержня обеспечивает выполнение такого условия, то задача растяжение / сжатие называется статически определимой. В противном случае, когда заданы 2 условия усилия, задача будет статически неопределимой.

- статически определима;

- статически неопределима.

Постановка задач перемещения более трудоемка, но и является более общей. Она позволяет решать как статически определимую так и статически неопределимые задачи. Наиболее удобна для решения таких задач матричная формулировка метода начальных параметров.

Введем понятие вектора состояния следующим образом:

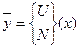(2.10)

Сопоставим с ним уравнения (2.3) и (2.5)

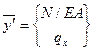
Интегрируя это уравнение, получим

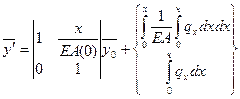
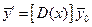будем называть матрицей влияния

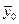- вектор начальных параметров;

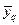- вектор влияния распределенной нагрузк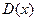и.

и 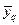представляют собой решение уравнений состояния при растяжении.

Из формулы (2.11) ясно, что для конца участка стержня вектор состояния определяется формулой:

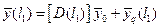(2.12)

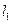- длина участка.

Допустим, стержень состоит из двух участков. Мысленно отсечем первый участок и будем считать, что в начале второго участка состояний 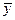определено формулой (2.12).

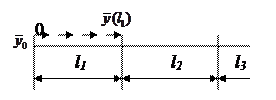
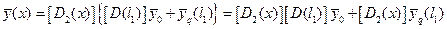
Продолжая эту формулу по индукции, получим, что в точке, принадлежащей участку с номером n, вектор состояния можно найти по формуле:

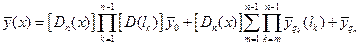(2.13)

Первое слагаемое представляет собой влияние начальных параметров на состояние произвольного участка, второе – влияние распределенных нагрузок на предыдущих участках, последнее – влияние распределенной нагрузки на n-ом участке.

Допустим, в начальном участке задана сосредоточенная продольная сила. Ее влияние на состояние описывается вектором:

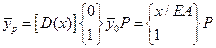(2.14)

Тогда (2.12) следует дополнить слагаемым, которое будет учитывать влияние сосредоточенных сил, заданных на границах всех предыдущих участков.

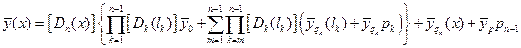(2.15)

Запишем значения обеих частей и (2.15.) для конца стержня:

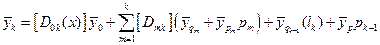(2.16)

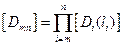- матрица влияния узла на узел.

Формула (2.16) содержит вектор параметров 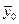, подлежащий определению. Одна из его компонент - или сила, или перемещение - известны из краевого условия в начале стержня.

Например:

Если стержень заделан в жесткую опору, то известно, что

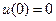
Если на конце стержня заданы силы, то условие выглядит так:

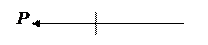
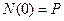
Краевые условия при растяжении/сжатии определены и на начале стержня (1 условие) и в его конце (2 условие).

Так как из условия в начале стержня известен один из начальных параметров (перемещение или усилие), то в (2.16) остается только одно неизвестное. Для его определения выбирают то из двух уравнений, в котором известна одна из компонент .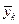

Определив эту компоненту можно построить эпюры продольных сил и перемещение, пользуясь (2.15).

Метод начальных параметров легко реализуется на любом математическом пакете. Достаточно написать функции, вычислить матрицы влияния и векторы влияния распределенных и сосредоточенных нагрузок, а после функцию, вычисляющую матрицу и правую часть (2.16). Выбор разрешающего уравнения при работе с математическими пакетами удобно сделать вручную.