КИНЕМАТИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

Под словом «благотворительность» в старину понималось сострадание к ближнему, милосердие. Для нуждающихся строились различные богоугодные заведения - больницы, приюты, школы, училища, богадельни. Благотворительность была одной из главнейших добродетелей христианства. В дореволюционной России благотворитель-ность обычно не включалась в государственные программы помощи бедным, ею занимались частные лица и общества помощи нуждающимся. Государственная же помощь обозначалась термином «призрение» (обще-ственное призрение). Благотворительность была широко распространена в государственной и общественной жизни России. Еще при князе Владимире нищие и убогие могли приходить на княжеский двор и получать там «всякую потребу, питье и яствы...». В 18 в. масштабы российской благотворительности значительно возросли. В 1775 г. в составе новых губернских учреждений появился особый приказ общественного призрения. На него возлагалась забота об образовании, лечении, устройстве народных школ, сиротских домов, приютов и богаделен для престарелых, работных и смирительных домов. Через 65 лет в стране таких учреждений было уже около 800. В 1860-1870 гг. забота об общественном призрении передавалась земствам и городам. В Москве в 1894 г. повсюду были учреждены участковые попечительства о бедных. Москва занимала особое место в истории российского благотворительства. В екатерининскую эпоху здесь были открыты воспитательный дом (1763), Вдовий дом (1772), Екатерининская (1776) и Голицынская (1801) больницы, Шереметевский странноприимный дом (1810) и многие другие крупные благотворительные учреждения, зачастую строившиеся по проектам знаменитых архитекторов (Голицынская больница М. Ф. Казакова). Подъем и расцвет благотворительности во вт. пол. 18 — пер. трети 19 в. стали следствием дворянской филантропии (человеколюбия). Строительство больниц, приютов, богаделен для бедного населения было делом чести, престижа. Богатые дворяне Д.М. Голицын, Н.П. Шереметев, А.Н. Стрекалова и другие жертвовали огромные средства на устройство различных богоугодных заведений. Система благотворительности в старой России отличалась разнообразием форм учреждений и обществ. Полуправительственный, полуобщественный характер носила деятельность заведений Ведомства учреждений императрицы Марии (1796), названного так по имени супруги императора Павла I. К 1900 г, в Ведомстве Марии состояло более 500 учебных и благотворительных заведений, где жили, обучались, лечились десятки тысяч людей. К крупнейшим учреждениям Ведомства Марии относились совет детских приютов, дамское попечительство о бедных, так называемые Мариинские больницы для бедных и др. Параллельно с Ведомством Марии в России существовало созданное в 1802 г. по инициативе Александра I Филантропическое (с 1816 г. — Человеколюбивое) общество, главной целью которого было оказание добровольной разносторонней помощи бедным. В Москве в систему этого общества входили известные богадельни — Маросейская, Набилковская, Черкасская и др. Широкий размах в России имела церковная благотворительность. Только в Москве в начале 20 в. насчитывалось 69 церковных попечительств бедных. На содержании московских приходских храмов состояло более 100 небольших богаделен. Особое значение в системе частной благотворительности имели сословные учреждения. В Москве на средства дворян, купца», священников организовывались учебные заведения, приюты, богадельни, где учились или жили представители данного сословия. Российская государственная и частная благотворительность со второй половины 19 в. существовала в основном на пожертвования купечества. Особенно велики заслуги этого сословия для развития благотворительных учреждений в Москве. Представители известных купеческих династий: Алексеевы, Бахрушины, Баевы, Боевы, Лямины, Мазурины, Морозовы, Солодовниковы, Хлудовы и другие — построили на свои средства десятки благотворительных учреждений и заведений, снабдили их современным по тем временам медицинским оборудованием. Всего в Москве к началу 20 в. насчитывалось 628 благотворительных заведений: богаделен, приютов, временных убежищ и общежитий, ночлежных домов, бесплатных и дешевых столовых и чайных, домов трудолюбия, общин сестер милосердия, амбулаторий и т. д. Формы помощи в них отличались также большим разнообразием: предоставление жилья, ночлега, бесплатных обедов, выдача единовременных или постоянных денежных и натурных пособий, врачебная помощь, оплата лекарств. Приблизительно такую же структуру имела и благотво-рительность в др. городах Российской империи. Важнейшей частью широкой благотворительности было меценатство, сыгравшее огромную роль в формировании и развитии отечественной культуры. Слово «меценатство» происходит от имени римского государственного деятеля Гая Цильния Мецената, жившего в 1 в. до н. э. и помогавшего талантливым римским поэтам того времени. Имя Мецената, как поклонника изящных искусств и покровителя поэтов, стало нарицательным и вошло в языки многих народов мира. Меценатами мы называем людей, добровольно жертвующих деньги, состояние и т. д. на построение различных общественных сооружений (храмов, театров, больниц, учебных заведений), помогающих художникам, писателям, поэтам, музыкантам. «Для того чтобы процветало искусство, - писал К. С. Станиславский, — нужны не только художники, но и меценаты». Именно усилиями меценатов в России создавались обширные собрания высокохудожественных памятников искусства, музеи, театры и другие центры духовной жизни. Меценатство как поддержка частными лицами культуры, науки и искусства получило развитие в России с 18 в., когда в стране возникли предпосылки для образовательной, музейно-собирательной и памятнико-охранительской деятельности. В городских дворцах и загородных дворянских усадьбах собирались замечательные коллекции памятников западноевропейского искусства, обширные библиотеки. Однако лишь отдельные представители российской аристократии 19 — н. 20 в. — Н.И. Румянцев, А. С. Уваров и П. С. Уварова, М. К. Тенишева, Ю. С. Нечаев-Мальцев и другие дарили свои коллекции государству или жертвовали большие средства на устройство новых музеев. Расцвет меценатства наступил во второй половине 19 в. благодаря российскому купечеству, придерживавшемуся православных традиций помощи ближнему и поддержки культурных общественных учреждений. Нередко меценатство становилось обязательным для многих купеческих семей. Каждый большой и малый город имел таких покровителей, но московские меценаты славились по всей России. Знаменитый род промышленников Морозовых оставил после себя множество памятников культурно-просветительской деятельности. Так, на средства Марии Федоровны и Феодосии Ермиловны Морозовых строились и украшались многие старообрядческие храмы, Сергей Тимофеевич Морозов построил в Леонтьевском переулке Кустарный музей, а Савва Тимофеевич — великолепное здание Художественного театра. Не менее известными покровителями культуры были и московские купцы Щукины. Меценатство и коллекционирование - давняя традиция этой семьи. Петр Иванович, собравший огромную коллекцию памятников русского искусства, выстроил на свои деньги здание музея на Грузинской улице, а затем в 1905 г. подарил его Историческому музею с собранием насчитывавший около 24 тыс. предметов! Его брат Сергей Иванович собрал замечательную по полноте коллекцию современной западноевропейской живописи, ставшую позже украшением Музея изобразительных искусств им. А. С. Пушкина. Основу крупнейшего в мире музея русского искусства — Третьяковской галереи составила коллекция купца Павла Михайловича Третьякова, переданная им в 1892 г. в дар Москве. Крупный железнодорожный промышленник Савва Иванович Мамонтов, человек разносторонне одаренный, большой знаток и ценитель искусства, создал в своем имении Абрамцево своеобразный творческий кружок, объединявший таких талантливых мастеров русского искусства, как В. Д. Поленов, М. А. Врубель, В. М. Васнецов, В. А. Серов и другие. На сцене Частной оперы в Москве, основанной на средства Мамонтова, расцвел гениальный дар Ф. И. Шаляпина.

КИНЕМАТИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

Колебательное движение. Общие условия возникновения и существования колебаний.Движение веток в ветреную погоду, маятника часов, смычка скрипача, крыльев птиц повторяется через определенные промежутки времени. Такие многократно повторяющиеся движения называют колебательными движениями, или, кратко, колебаниями.

Колебания свойственны всем явлениям природы: пульсирует излучение звёзд, внутри которых происходят циклические ядерные реакции; с высокой степенью периодичности вращаются планеты Солнечной системы; движение Луны вызывает приливы и отливы на Земле; ветры возбуждают колебания и волны на поверхностях водоёмов. Внутри любого живого организма - от одиночной клетки до высокоорганизованных их популяций - непрерывно происходят разнообразные, ритмично повторяющиеся процессы: биение сердца, колебания психических состояний и др. В виде сложнейшей совокупности колебаний частиц и полей (электронов, фотонов, протонов и др.) можно представить «устройство» микромира.

В физике особо выделяются колебания двух видов - механические и электромагнитные. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в масштабах, характерных для жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большую часть прямой информации об окружающем мире.

Колебания любых физических величин почти всегда сопровождаются попеременным превращением энергии одного вида в энергию другого вида. Так, оттягивая маятник от положения равновесия, мы увеличиваем потенциальную энергию груза, запасённую в поле тяжести; при отпускании он начинает падать, вращаясь около точки подвеса как около центра, и в крайнем нижнем положении вся потенциальная энергия превращается в кинетическую. Поэтому груз проскакивает это равновесное положение, и процесс перекачки энергии повторяется, пока рассеяние энергии, обусловленное, например, трением, не приведёт к полному прекращению колебаний.

Для того чтобы совершалось колебательное движение необходимо 1) чтобы одним из возможных положений тела было положение его устойчивого равновесия; 2) после того как тело выведено из положения устойчивого равновесия, должна появиться сила, возвращающая его в исходное состояние.

1.2.2. Параметры колебательного движения.Самый характер движений определяет и те вопросы, которыми обычно интересуются при изучении колебаний. При изучении неповторяющихся движений мы чаще всего интересуемся положением, скоростью и ускорением движущихся тел в какой-то момент времени. В колебательном движении нас главным образом интересует уже не состояние системы в данный момент времени, а признаки, характеризующие повторяемость движения. Это - закон, по которому повторяется движение, время, через которое система снова приходит к тому же самому состоянию, наибольшие отклонения, которых достигает движущееся тело.

Для рассмотрения колебательного процесса удобен геометрический способ представления, который сводится к следующему (рис. 1.1).

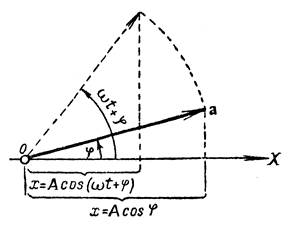
Рис. 1.1.Представление гармонического колебательного движения как движения проекции вектора 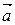, вращающегося с постоянной угловой скоростью

Возьмем ось, назовем ее осью 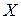и выберем на ней произвольную точку 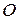. Из этой точки под углом 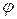отложим вектор 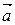, величина которого 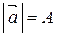. Спроецируем конец вектора на ось 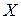. Из рисунка видно, что координата точки, в которую спроецировался конец вектора 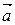, равна

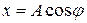. (1.1)

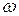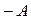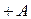Будем равномерно вращать вектор с угловой скоростью против часовой стрелки. Тогда координата конца вектора будет изменяться в пределах от до . Для произвольного момента времени 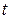вектор образует с осью 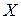угол, равный 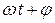, при этом координата конца вектора будет равна

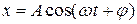. (1.2)

Мы видим, что координата конца вектора или, что то же самое, величина проекции вектора на некоторую ось будет совершать колебательное движение, т. к. время входит в (1.2) через периодическую функцию. Это значит, что существует такой интервал времени 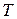, что

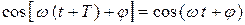. (1.3)

Промежуток времени, в течение которого совершается одно полное колебание, называется периодом колебаний 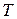.Обратная величина периода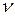

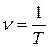(1.4)

называется линейной частотой. Линейная частота измеряется в герцах; 1 Гц – частота такого периодического процесса, период которого равен 1 с. Из (1.3) следует, что

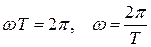. (1.5)

Величина 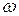называется круговой (циклической) частотой колебаний. Она измеряется в радианах в секунду 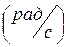. Сравнивая (1.4) и (1.5), получим связь между 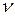и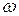

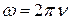. (1.6)

Множитель 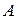в (1.2) определяет максимальное значение колеблющейся величины и называется амплитудой колебаний, аргумент косинуса 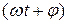- фазой, а постоянная 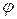- начальной(в момент времени 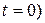фазой колебания. Можно сказать, что фазой колебания называют величину, определяющую в данный момент времени (совместно с амплитудой) значение колеблющейся величины и измеряемую промежутком времени (в долях периода), истекшим от начала колебательного процесса.

1.2.3. Гармонические колебания.Колебательное движение, при котором физическая величина изменяется с течением времени по закону синуса или косинуса, называется гармоническим колебательным движением или просто гармоническим колебанием. Ни в природе, ни в технике никогда не встречаются строго периодические гармонические колебания. Тем не менее, изучение гармонических колебаний очень важно по двум основным причинам: 1) в природе и в технических устройствах часто возникают колебания, мало отличающиеся на протяжении достаточно большого промежутка времени от гармонических; 2) существует очень широкий класс физических систем (т. н. спектральные приборы), которые преобразуют произвольные (негармонические) колебания в набор колебаний, близких к гармоническим, осуществляя гармонический анализ.

1.2.4. Скорость и ускорение при гармоническом колебательном движении. Если точка совершает гармонические колебания, то ее смещение 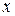равно:

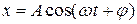. (1.7)

Скорость 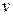численно равна производной по времени от смещения:

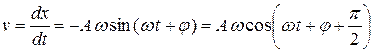. (1.8)

Ускорение точки можно получить, взяв производную от скорости по времени:

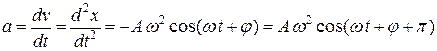. (1.9)

Из формул (1.8) и (1.9) видно, что скорость и ускорение точки, совершающей гармонические колебания, также изменяются по гармоническому закону с той же частотой. При этом амплитуда скорости 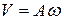, а амплитуда ускорения 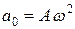. По фазе скорость сдвинута на 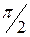, а ускорение – на 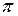относительно смещения.

Равенство (1.9) на основании (1.7) может быть переписано:

.

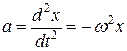Мы видим, что ускорение при гармоническом колебании пропорционально смещению 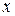и направлено к положению равновесия. Уравнение

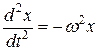
или в каноническом виде

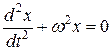(1.10)

носит название дифференциального уравнения гармонических колебаний.