ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Если на тело действует колеблющаяся по величине внешняя сила, то тело будет совершать колебания, характер которых повторяет характер изменений внешней силы. Такие колебания называются вынужденными.
Пусть на осциллятор (п. 3.2.1.) помимо упругой силы 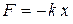 и силы трения
и силы трения 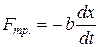 действует еще и внешняя сила, зависимость которой от времени выражается формулой
действует еще и внешняя сила, зависимость которой от времени выражается формулой

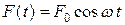 (4.1)
(4.1)
где 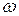 – круговая частота изменения внешней силы, вообще говоря, отличная от частоты
– круговая частота изменения внешней силы, вообще говоря, отличная от частоты 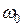 собственных колебаний осциллятора,
собственных колебаний осциллятора, 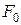 – амплитуда силы. Сейчас мы будем изучать картину установившихся под действием этой силы колебанийи не будем интересоваться переходным процессом, протекающим от момента включения (4.1) до установления регулярных колебаний.
– амплитуда силы. Сейчас мы будем изучать картину установившихся под действием этой силы колебанийи не будем интересоваться переходным процессом, протекающим от момента включения (4.1) до установления регулярных колебаний.
Уравнение движения в форме второго закона Ньютона имеет вид:
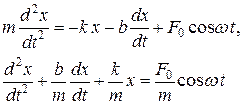 (4.2)
(4.2)
Введем привычные обозначения:
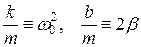 , и
, и 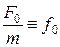
и перепишем уравнение:
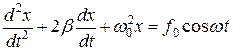 (4.3)
(4.3)
Интересующие нас установившиеся вынужденные колебания происходят по гармоническому закону с частотой, равной частоте внешней силы, т. е.
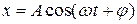 . (4.4)
. (4.4)
Чтобы определить амплитуду 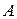 и фазу
и фазу 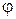 этих вынужденных колебаний, подставим решение (4.4) в уравнение (4.3):
этих вынужденных колебаний, подставим решение (4.4) в уравнение (4.3):
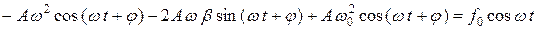 ,
,
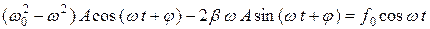 . (4.5)
. (4.5)
Воспользуемся формулами тригонометрии:
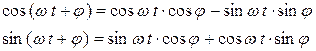
и соберем вместе члены, содержащие синусы и косинусы аргумента 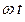 :
:
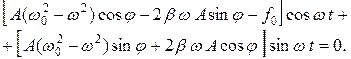 (4.6)
(4.6)
Для того чтобы (4.6) представляло собой тождество, необходимо чтобы коэффициенты при множителях 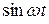 и
и 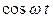 были независимо равны нулю. Таким образом, мы получаем систему двух уравнений для определения неизвестных величин
были независимо равны нулю. Таким образом, мы получаем систему двух уравнений для определения неизвестных величин 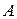 и
и 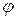 :
:
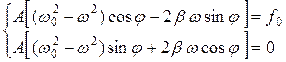 (4.7)
(4.7)
Чтобы найти 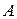 , возведем оба уравнения в квадрат и сложим:
, возведем оба уравнения в квадрат и сложим:
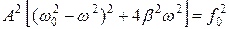 ,
,
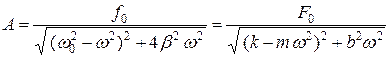 . (4.8)
. (4.8)
Фазу 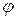 найдем из второго уравнения системы (4.7):
найдем из второго уравнения системы (4.7):
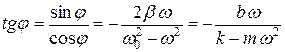 . (4.9)
. (4.9)
4.2.2. Анализ решения для амплитуды. Резонанс. Сначала выясним, как ведет себя амплитуда вынужденных колебаний при частотах внешнего воздействия 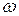 близких и далеких от частоты собственных колебаний системы
близких и далеких от частоты собственных колебаний системы
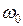 в случае, когда затухание колебаний мало, т. е.
в случае, когда затухание колебаний мало, т. е. 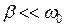 . Из (4.8) имеем:
. Из (4.8) имеем:
а) при 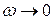 :
:
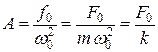 . (4.10)
. (4.10)
Амплитуда вынужденных колебаний равна величине статического смещения, которое вызвала бы постоянная по величине сила 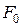 ;
;
б) при 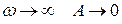 ;
;
в) при 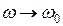 и
и 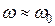 ,
,
когда частота внешнего воздействия приближается к частоте 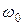 собственных колебаний системы, величина
собственных колебаний системы, величина 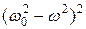 уменьшается. При этом знаменатель (4.8) стремится к наименьшему значению, амплитуда возрастает и проходит через максимум при условии:
уменьшается. При этом знаменатель (4.8) стремится к наименьшему значению, амплитуда возрастает и проходит через максимум при условии: 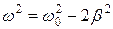 , т. е. когда
, т. е. когда 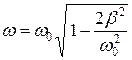 , что при условии малости затухания
, что при условии малости затухания 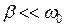 сводится к приближенному равенству
сводится к приближенному равенству 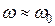 . В этом случае:
. В этом случае:
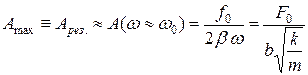 . (4.11)
. (4.11)
Используя декремент затухания 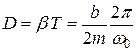 , откуда
, откуда 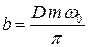 , имеем:
, имеем:
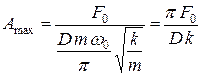 . (4.12)
. (4.12)
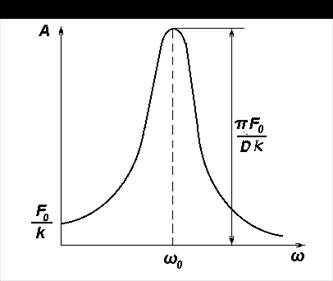
Рис. 4.1. Амплитудная резонансная кривая
Во сколько раз амплитуда в максимуме превосходит статическое (при 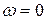 ) значение? Разделим (4.12) на (4.10):
) значение? Разделим (4.12) на (4.10):
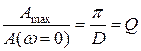 . (4.13)
. (4.13)
Отношение амплитуд определяется добротностью колебательной системы. Если добротность велика, то наибольшая амплитуда вынужденных колебаний во много раз превышает статическое отклонение.
Это резкое увеличение амплитуд вынужденных колебаний в области, где частота вынуждающей силы 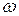 близка к частоте собственных колебаний системы
близка к частоте собственных колебаний системы 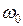 , представляет собой наиболее характерную черту явления резонанса. Отметим, что во всех случаях
, представляет собой наиболее характерную черту явления резонанса. Отметим, что во всех случаях 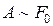 , т. е. амплитуда вынужденных колебаний линейно зависит от амплитуды силы, вынуждающей колебания. Семейство кривых
, т. е. амплитуда вынужденных колебаний линейно зависит от амплитуды силы, вынуждающей колебания. Семейство кривых 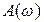 на рис. 4.2 соответствует разным значениям затухания. Это – амплитудные резонансные кривые.
на рис. 4.2 соответствует разным значениям затухания. Это – амплитудные резонансные кривые.
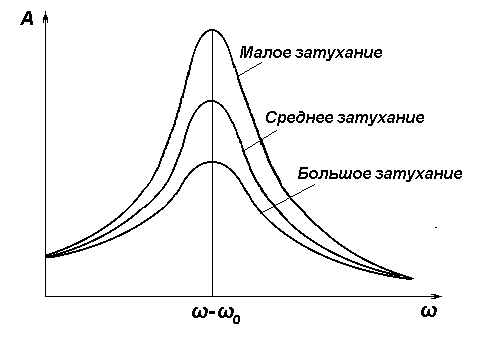
Рис. 4.2.Семейство амплитудных резонансных кривых при различном затухании
4.2.3. Анализ решения для фазы. Соотношение (4.9) позволяет проследить за изменением сдвига фаз 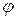 при изменении частоты внешнего воздействия
при изменении частоты внешнего воздействия 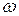 . Для удобства рассуждений сведем воедино необходимые формулы:
. Для удобства рассуждений сведем воедино необходимые формулы:
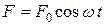 , (4.1)
, (4.1)
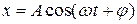 , (4.4)
, (4.4)
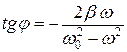 . (4.9)
. (4.9)
а) При условии 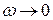 ,
,
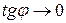 и
и 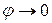 . Фаза вынужденных колебаний примерно совпадает с фазой внешней силы.
. Фаза вынужденных колебаний примерно совпадает с фазой внешней силы.
б) При 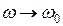 ,
,
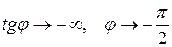 . Колебание при резонансе отстает на
. Колебание при резонансе отстает на 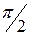 от фазы внешней силы.
от фазы внешней силы.
в) При 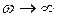 ,
,
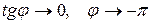 . Колебание находится в противофазе с силой.
. Колебание находится в противофазе с силой.
График зависимости 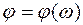 представлен на рис. 4.3.
представлен на рис. 4.3.
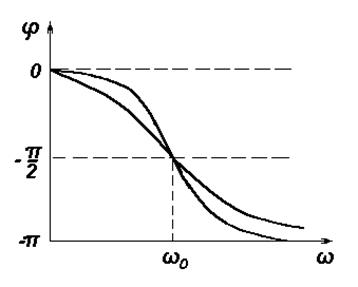
Рис. 4.3. Семейство фазовых резонансных кривых
Это – фазовые резонансные кривые. Если декремент затухания мал, то в области резонанса происходят резкие изменения фазы. В небольшом диапазоне изменения частот сдвиг фаз меняется на p. Составим таблицу.
Таблица. Сдвиг фаз между внешней силой 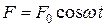 и колебанием
и колебанием 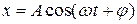 .
.
| Название параметра | Значения частоты 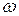
| ||
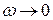
| 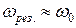
| 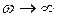
| |
Смещение 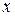 , фаза , фаза 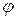
| 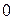
| 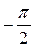
| 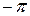
|
Скорость 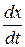 , фаза , фаза 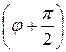
| 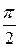
| 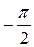
| |
Ускорение 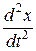 , фаза , фаза 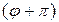
| 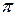
| 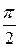
|
4.2.4. Вынужденные колебания в электрических цепях. Вынужденные колебания в электрическом контуре возникают при наличии в нем внешнего источника с периодически меняющейся ЭДС (рис. 4.4) или какого-либо произвольного внешнего источника переменного напряжения 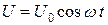 , (4.14)
, (4.14)
где 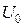 – амплитудное (максимальное) значение напряжения. В этом случае дифференциальное уравнение (3.17) с учетом (4.14) запишется в виде:
– амплитудное (максимальное) значение напряжения. В этом случае дифференциальное уравнение (3.17) с учетом (4.14) запишется в виде:
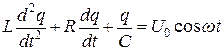 . (4.15)
. (4.15)
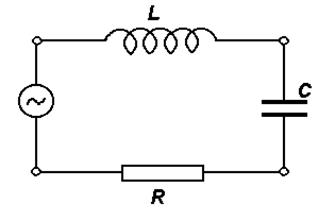
Рис. 4.4. Схема электрического колебательного контура с источником внешней ЭДС
Разделив все члены уравнения (4.15) на 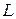 и введя прежние обозначения
и введя прежние обозначения
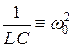 , (3.18)
, (3.18)
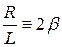 , (3.19)
, (3.19)
а также 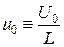 , (4.16)
, (4.16)
придем к уравнению
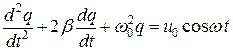 . (4.17)
. (4.17)
Как и в случае с механической системой мы будем интересоваться установившимисяпод действием внешнего периодически меняющегося напряжения вынужденными колебаниями, т. е. предположим, что заряд конденсатора будет изменяться во времени с частотой 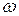 по закону:
по закону:
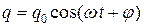 . (4.18)
. (4.18)
Повторяя полностью рассуждения, связанные с решением уравнения для установившихся вынужденных механических колебаний (в этом заключается плодотворность единого подхода см. п. 2.2.4), мы придем к следующим формулам для величин 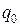 и
и 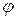 :
:
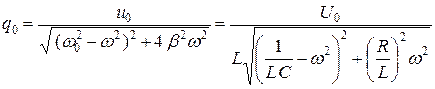 , (4.19)
, (4.19)
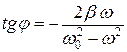 . (4.20)
. (4.20)
Дата добавления: 2015-01-19; просмотров: 3047;
