Вынужденные колебания.
Дифференциальные уравнения (3-20), (3-22), (3-23) дают возможность рассчитать параметры вынужденных колебаний. При этом правая часть характеризует собственные свойства системы, а левая часть описывает внешние воздействия. Механизм разным образом реагирует на внешние воздействия.
Если внешнее воздействие изменяется скачком, то реакция называется переходным процессом и описывается выражениями типа (3-55), (3-56).
Если внешнее воздействие изменяется по гармоническому закону, например F(t)= Fа sin(wt), то реакцию механизма удобней исследовать с помощью частотных характеристик. Они получаются преобразованием по Лапласу исходных уравнений, т.е. переходом к уравнениям типа
B(s)F(s)= (T2 s2 + 2x Tи s+1) x(s).
Замена оператора Лапласа s= jw позволяет записать выражение
B(jw)F(jw)= [T2 (jw)2 + 2x Tи jw +1] x(jw),
с помощью которого определяются частотные характеристики
W( jw)= x(jw)/F(jw)= B(jw)/[T2 (jw)2 + 2x Tи jw +1], (3-78)
где B(jw)= b0+ b1(jw)+…+ bn (jw)n-1.
Из этого выражения можно определить амплитуду колебаний выходной координаты
x(w)= Fa ½B(w)½/[(1- T2w2)2+ (2x Tи w)2]1/2. (3-79)
и фазу колебаний
j= arg B(w)- arctg[2x Tи w/(1- T2 w2)]. (3-80)
Из (3-79) следует, что при w= Т-1 в системе наступает резонанс.
О динамических свойствах исследуемой системы судят по ее реакции на стандартные воздействия: скачок, гармонический сигнал, импульсную функцию, а также по частотным характеристикам (рис. 3.14), с помощью которых можно определить частотную зону резонанса или амплитуду колебаний выходной координаты под действием известного входного гармонического воздействия.
Таким образом, амплитуда колебаний при коротких магистралях определяется с помощью выражений:
для продольных колебаний
при Fº 0
|u(w)|=u1а (1-c) /[(1-с- mJп0w)2+ (hnJ п0 w)2]1/2 , (3-81)
|s2 (w)|=u1а(1-с)-1f-12[hn2 +(mw)2]1/2/[(1-с- mJп0w)2+
+ (hnJ п0 w)2]1/2, (3-82)
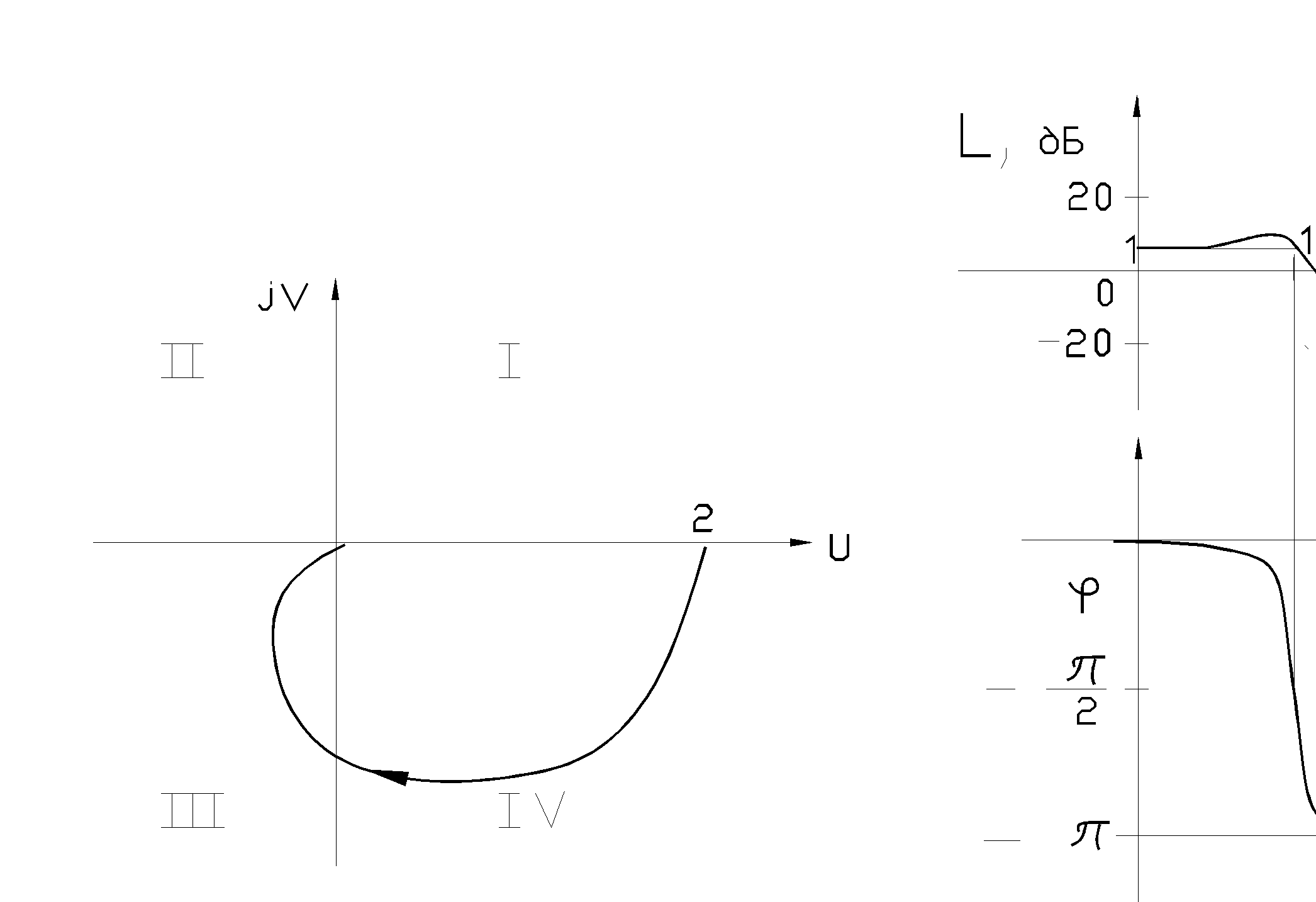
а) б)
Рис. 3.14 Амплитудно- фазовая (а) и логарифмические амплитудная и фазовая частотные характеристики колебательного звена.
при u1 º 0
|u(w)|=Fа Jп0w /[(1-с- mJп0w)2+ (hnJ п0 w)2]1/2 ; (3-83)
|s2 (w)|=Fа (1-с)-1f -12 /[(1-с- mJп0w)2+ (hnJ п0 w)2]1/2, (3-84)
для крутильных колебаний
при Мкрº 0
|W2аW|= W1a/{[1- Т2k w 2]2+[2zkТkw]2}0,5, (3-85)
|tаW|=W1a hk W -1p2[1+ (Тиkw)2]1/2/{[1- Т2k w 2]2+[2zkТk)w]2}0,5, (3-86)
при W1º 0
|W2аМ|= Мa çJ k(w)çw/{[1- Т2k Z k(jw) w 2]2+[2zkТk Zk(jw)w]2}0,5 , (3-87)
|tаМ|= МaW-1p2/{[1- Т2k Z k(jw) w 2]2+[2zkТп Zk(jw)w]2}0,5 (3-88)
где 2zkТk= hkJk0; Тk= (JJk0)1/2; zk= 0,5Jk0hk [mJ п0]-1/2; hk= ¶ Mтр /¶W2.
Пример 3.4. Рассчитать частотные характеристики и определить резонансную частоту механизма на рис.3.15 при поперечных колебаниях диска, например шестерни, возникающих во время передачи мощности к зубчатому колесу.
Параметры механизма:
диаметр стального вала d= 20 мм; a= 100 мм; a= b; E= 2*105 Н/мм2; плотность стали r= 7, 8*10-3 кг/см3; диаметр диска D= 100 мм; ширина B= 20 мм; h=1 Hc/ мм.
Определим массу диска
m= BgpD2/(4g)= p*2*7,8*10-3*102/4= 1,225 кг.
Далее mg= 1,225*9,8= 12 Н.
F
Рис. 3.15
Схема механизма
a b
Определим момент инерции сечения вала
J= pd4/64= p (2*10-2)4/64= 0,785*10-8м4=
= 0,785*10-8*1012=0,785*104мм4 .
Определим прогиб вала от веса диска
yст= mga2b2/(3E J l)= 12*108 /(3*2*105*0,785*104*2*102)=
=1,274*10-3мм..
Вычислим коффициент упругости
J= [ycm/(mg)] = 1,274*10-3/12= 0,106*10-3 мм/Н = 0,106*10-6 с2/кг.
Выражение для частотной характеристики, характеризующей влияние силы F на скорость движения при поперечных колебаниях диска, запишется в форме
W(jw)= u(jw)/F(jw)= - jwJ/[1+ Jhjw+ Jm(jw)2] =
= - jw0,106*10-3/[1+0,106*10-3jw+ 0,106*10-3*120(jw)2].
Откуда круговая резонансная частота
wрез= (Jm)-1/2=(0,106*10-6*1,225)-1/2=2775 рад/сек.
Для построения частотных характеристик запишем уравнения мнимой и вещественной частей, амплитудной и фазовой характеристик
Таблица 3.3
Построение частотных характеристик
| №№ | w, рад/с | U | V | A | L= 20lgA | j, град |
| 1,48*10-8 | 1,22*10-4 | 1,22*10-4 | -78,3 | |||
| 5*10-8 | 2,2*10-4 | 2,2*10-4 | -73 | |||
| 1,94*10-7 | 4,4*10-4 | 4,4*10-4 | -67 | |||
| 1*10-6 | 10-3 | 1*10-3 | -59,9 | |||
| 5*10-6 | 2,26*10-3 | 2,26*10-3 | -53 | |||
| 0,0063 | 0,0796 | 0,0796 | -22 | |||
| 1*10-5 | -3,3*10-3 | 3,3*10-3 | -49,5 | -89,8 | ||
| 3,5*10-7 | -1,9*10-3 | 1,9*10-3 | -54,5 | -90 | ||
| 1,5*10-7 | -3,9*10-4 | 3,9*10-4 | -68,8 | -90 |
V= -Jw(1- Jmw2)/[( 1- Jmw2)2+ (Jhw) 2] ;
U= - J2hw2/[( 1- Jmw2)2+ (Jhw) 2];
А= Jw./[( 1- Jmw2)2+ (Jhw) 2]1/2;
j = arctg[ (1- Jmw2)/ (Jhw)].
Заметим, что здесь А= |u(jw)/F(jw)| .
Частотные характеристики удобно строить, предварительно составив таблицу 3.3
На основании данных таблицы 3.3 построены логарифмические амплитудная и фазовая частотные характеристики (рис. 3.16,а) и амплитудно- частотная характеристика (рис. 3.16,б), где отчетливо виден резонансный всплеск.
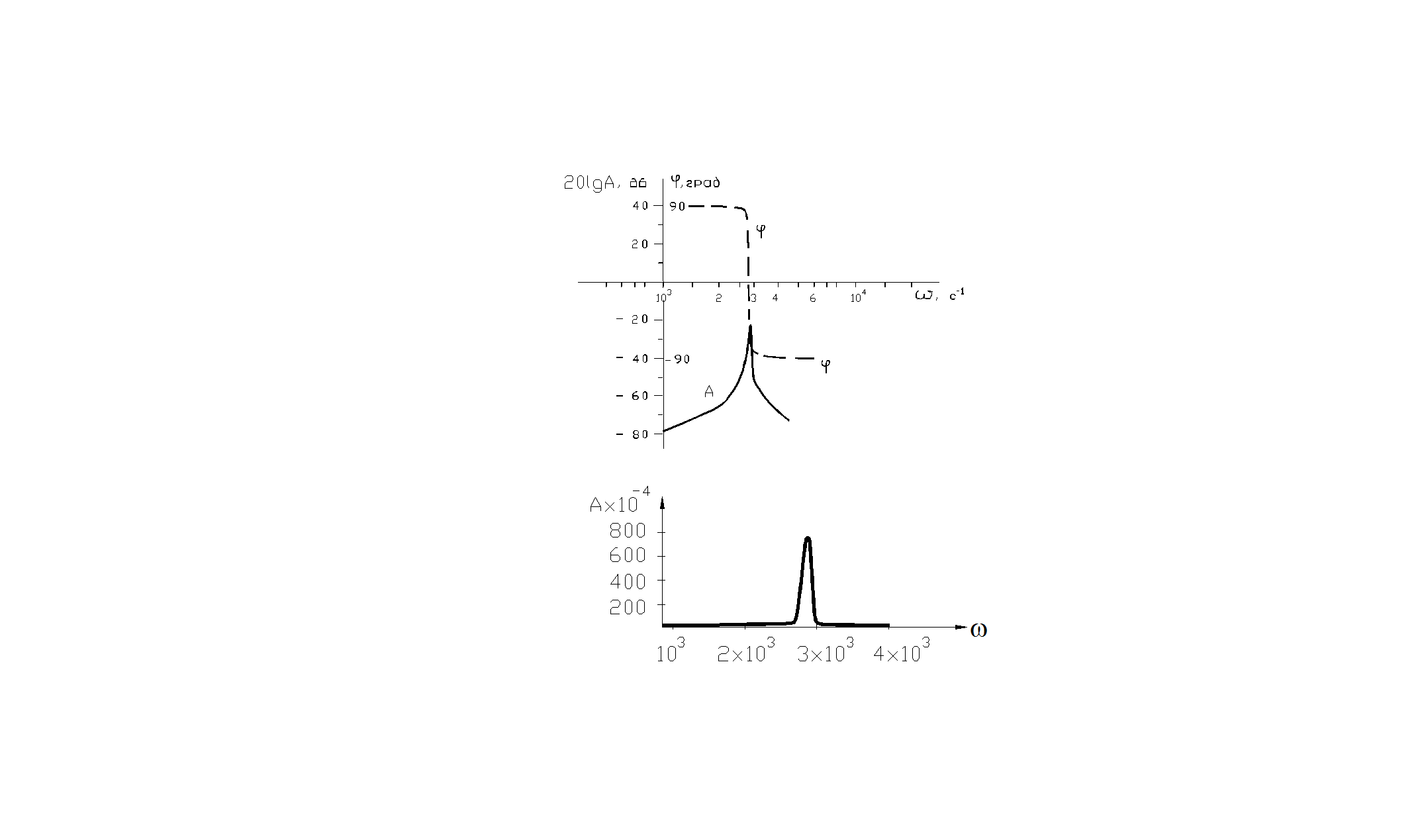
Рис.3.16
Частотные характеристики:
j- сдвиг по фазе;
А- амплитуда АФЧХ
а) логарифмические амплитудная и (А) и фазовая (j) частотные характеристики;
б) амплитудная частотная характеристика.
Пример 3.5.Исследовать динамические свойства подпружиненного механизма продольного перемещения (рис. 3.17). Подобные усторойства используются в тепловой энергетике в качестве упругих опор.
При анализе учтем формулы, приведенные в разделах 2.16 и 3.3.
Движение тела массой m опишем уравнениями[8]
u1(t) =u2 (t)+ Jпр0 fpsy(t); sy(t)f= F(t)+ hu2 (t)+ mpu2 (t). (3-89)
Первое уравнение, иллюстрирует закон сохранения количества движения, полученного системой тело- пружина от толкателя. Второе уравнение- второй закон Ньютона.
Под действием веса тела Р= mg и составляющей F1 развиваются силы трения Fтр. Поскольку известно, что трение зависит от контактного давления рк и скорости относительного движения трущихся поверхностей u2, то изменение силы
трения после разложения функции Fтр(рк ,u2) в ряд Тейлора можно представить выражением
DFтр= (¶Fтр/¶рк)Dрк+ (¶Fтр/¶u2)Du2= скDрк+ hDu2.
Второе слагаемое характеризует потери, пропорциональные скорости движения. Оно вошло в систему уравнений (3-89) в форме произведения hu2(t). Первое слагаемое преобразуем следующим образом скDрк @ cfsy.
Это слагаемое приводит к дополнительному увеличению напряжения в пружине площадью f. Причем в случае изменения направления движения знак этой составляющей силы меняется на противоположный. Для смазываемых минеральным маслом поверхностей принимают с= 0,025- 0,09. В этой связи, рассматривая малые отклонения, перепишем второе уравнение системы (3-89)
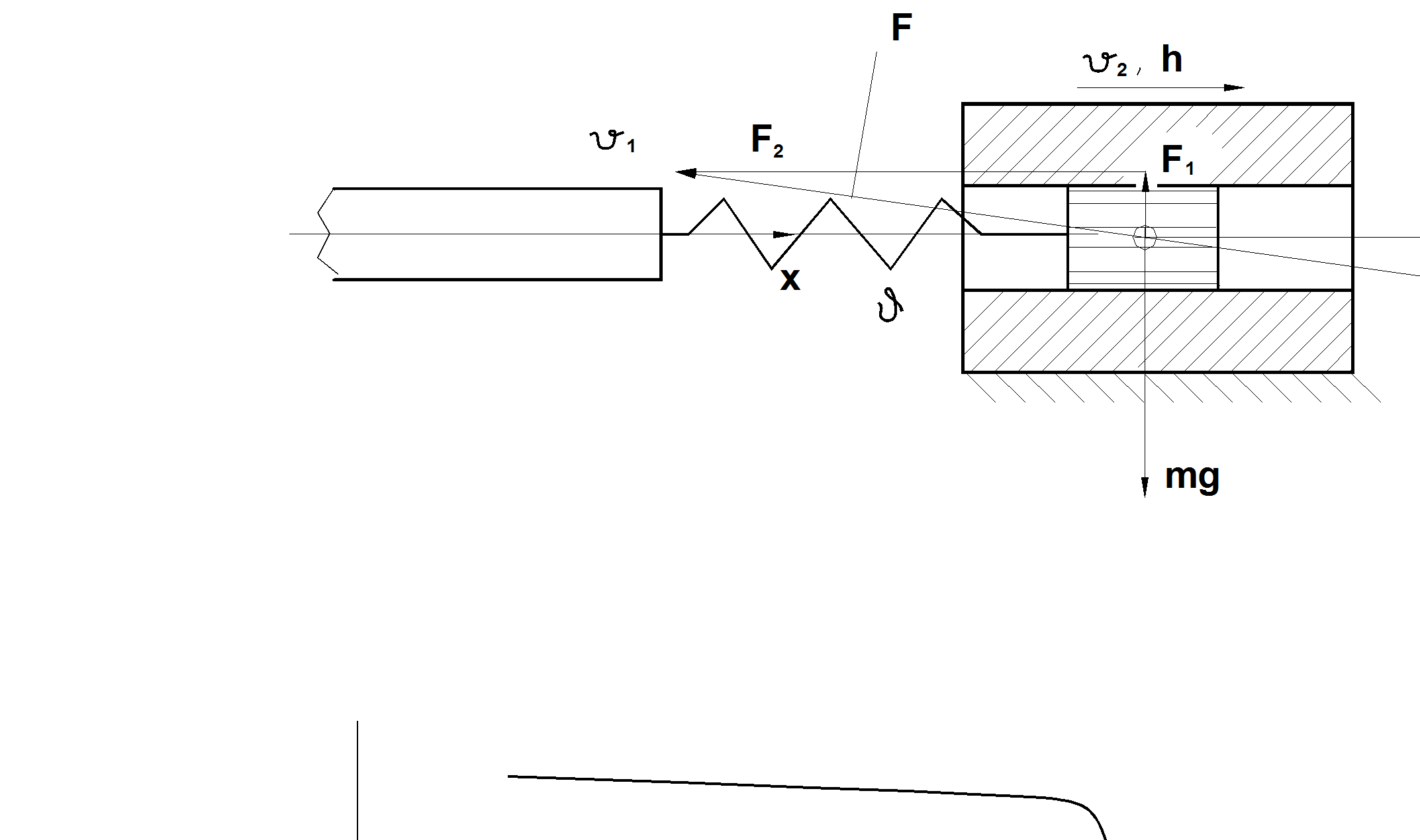
Рис. 3.17. Подпружиненный механизм.
sy(t)f(1- с sgnu2) = F(t)+ hu2 (t)+ mрu2. (3- 90)
Совместное решение (3-89) и (3-90) приводит к уравнению
u2 (t)(1- с sgnu2 )+ hJпр0 рu2 + mJпр0р2u2 = u1(t)(1- с sgnu2) – рF (t)Jпр0 . (3-91)
В случае знакопостоянной скорости u2 следует рассматривать уравнение
u2 (t)(1- с)+ hJпр0 рu2 + mJпр0р2u2 = u1(t)(1- с) – рF(t) Jпр0. (3-92)
Переходя к изображениям по Лапласу при нулевых начальных условиях, получим следующие передаточные функции
влияния u1 на u2 при Fº 0
Wu(s)= u2 (s)/u1 (s)= 1/[1+ 2z T s+ T 2 s2], (3-93)
влияния F на u2 при u1 º 0
Wu(s)= u2 (s)/F (s)=-(1-c)-1Jпр0 s/[1+ 2zT s+ T 2 s2], (3-94)
влияния u1 на напряжения в пружине при Fº 0
Wsu(s)= sу(s)/u1(s)=(1-c)-2hf-1(1+Tиs)/[1+2z T s+ T 2 s2], (3-95)
влияния F на u2 при u1 º 0
WsF(s)= sу(s)/F (s)= (1-с)-2 f-1/ [1+ 2z T s+ TuF s2], (3-96)
где T= [mJпр0 /(1-c)]1/2; z= 0,5hJпр0 /[T(1-c)] =0,5hJпр0 /[(1-c)mJпр0]1/2; Tи= m/h.
При этом резонансная частота
wрез= T -1.
Применив выше описанные методы, получим:
- при скачкообразном изменении скорости толкателя в случае F= 0
время быстродействия
tб= w-11 arctg (-a /w1). (3-97)
(Если потерями на трение можно пренебречь, то z=0, a=0 ибыстродействие tб= w-11p/2=1,57T. Это минимальное время быстродействия);
максимальную скорость
u2max= u10 [1+ exp(- a tm )]= u10 [1+ exp(-z T-1p kw -11)], (3-98)
где a=z / T ; w1= (1- z2)1/2 T-1 ; u10 - высота скачка (ступеньки).
(Очевидно, максимальное значение скорости будет при k=1, а затем величина ее всплесков станет уменьшаться);
- в случае скачкообразного изменения силы при u1=0
изменение скорости движения
u2 (t) = - F0(1-c)-1 f-1Jпр0 T-1sin(t T-1). (3-99)
изменение напряжения
sу(t) =(1-c)-2F0 f-1{1-[cos(w1 t)+ aFw-11 sin(w1 t)]exp(-a t)}. (3-100)
Максимум напряжения наблюдается при tm= kp /w1 (k=1, 3, 5 ...) и равен
sуmax = F0 (1-c)-2 f -1 [1+ exp(-p k/w1)]. (3-101)
При больших потерях на трение, когда z> 1, переходные характеристики не будут иметь резонансного всплеска
Если трение, пропорциональное скорости движения, имеет ярко выраженный нелинейный характер или в процессе работы механизма проявляются другие нелинейности, то анализ следует вести с помощью моделирования [6].
Пример 3.6. Имеется подъемно-транспортное устройство, которым совершается работа по перемещению какого-либо тела с помощью каната, содержащего металлический сердечник. Характеристика каната показана на рис. 3. 18
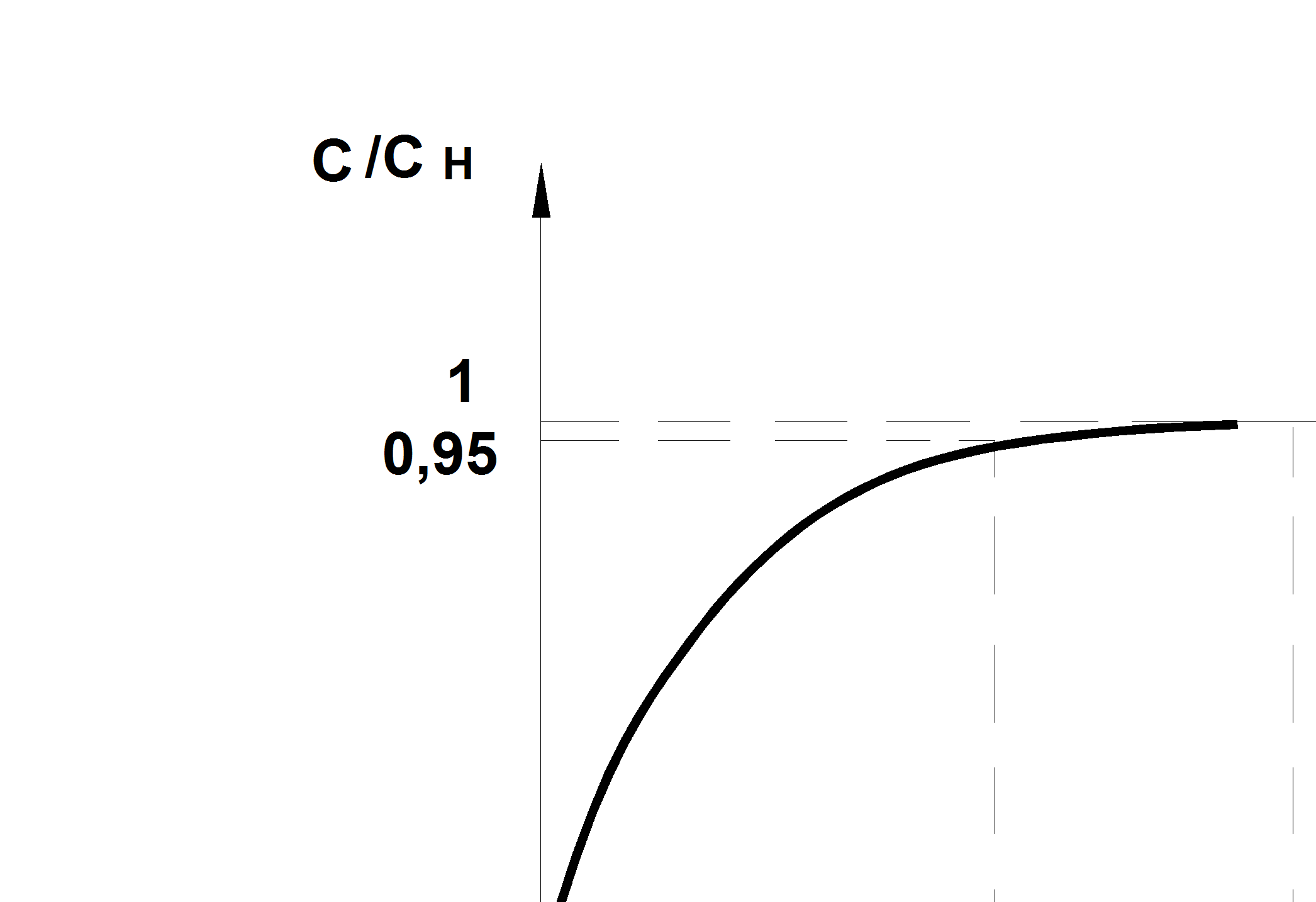
Рис. 3.18
Упругая характеристика
каната.
Здесь С, Сн- текущая и номинальная жесткость каната; F- усилие; Gн- номинальная нагрузка. Площадь сечения каната f= 100 мм2; Gн = 2*104Н.
На основании опубликованных данных[9] номинальный модуль упругости каната Ен= 1400 МПа.
По рис. 3.18 аппроксимируем характеристику выражением
C= Cн[1- exp(-5F/Gн)]= Cн[1- exp(-5fs /Gн)]. (3-102)
Полагая, что в канате при работе нет пластических деформаций, и применяя закон Гука, запишем s= Dх E/l= F/f.
Учитывая, что жесткость связана с перемещением и силой соотношением C= (Dх)-1F, получим Е= lC/f .
Умножим обе части равенства (3-102) на l/f (l - длина каната)
Е= Ен[1- exp(-5fs /Gн)]= 1,4*103[1- exp(- 0,025s)], (3-103)
где размерность [s]= МПа; [Е]= МПа.
Таким образом, текущий модуль упругости каната зависит от напряжения растяжения в его сечении.
Частотные характеристики будем строить по уравнению
u2(t)[1+ hJпрк(s)p+ mJпрк(s)р2]= eа u10 sin(w t- y). (3-104)
где eа - относительная амплитуда колебаний ведущего конца; y - сдвиг по фазе; Jпрк(s) = l/[E(s)f]- коэффициент упругости, зависящий от напряжений в канате.
Допустим, что напряжения изменяются в интервале [0; 120 МПа], т.е. изменения нагрузки будут F= 0… 1,2*104Н, начальная скорость перемещения, относительно которой происходят колебания, равна u10=10см/сек; коэффициент потерь на трение, пропорциональное скорости перемещения, h= 0,1 Нсек/см.

Рис. 3.19
Амплитудные частотные характеристики механизма с канатом:
а) А= 20 lg (`u2a / ea);
б) Аs= 20lg (s / ea)
Расчет[10] с помощью ПЭВМ будем вести по уравнению, полученному из (3-104)
Jпрк(s)mw2sin(wt)+ hJпрк(s)w cos(w t)+ sin(w t)=
= (ea /`u2a)[sin(wt)cosy- cos(w t)siny]. (3-105)
При sin(wt)=0, cos(w t)=1
hJпрк(s)w=-(ea /`u2a)siny , (3-106)
а при sin(wt)=1, cos(w t)=0-
- Jпрк(s)mw2)+1= (ea /`u2a)cosy. (3-107)
Возведем обе части уравнений в квадрат и сложим
(ea/`u2a)2=[-Jпрк(s)mw2+1]2+[hJпрк(s)w]2. (3-108)
Это уравнение является нелинейным из-за зависимости упругости от напряжения.
Разделив (3-106) на (3-107), получим фазовую характеристику
tgy= - hJпрк(s)w/[1-Jпрк(s)mw2] . (3-109)
Напряжение в магистрали определяется выражением
s(t)= [u2(t)h+ mdu2 /dt]/f.
Учитывая, что u2 =u2а sin(w t), получим
s(t)= [hu2а sin(w t) +w mu2а cos (w t)]/f.
Среднее значение изменения напряжения за четверть периода колебаний T/4= 2p /(4w) при y= w t = p /2 определим следующим образом
sср= (Т/4)-1  s(t) dt= (4w/ 2p)[-hu2af-1w-1cos(wt)|
s(t) dt= (4w/ 2p)[-hu2af-1w-1cos(wt)| 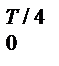 +
+
+ mu2af -1sin(wt)| 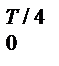 ]= 2u2af-1p -1(h+ mw)@ 2u2af-1p -1mw. (3-110)
]= 2u2af-1p -1(h+ mw)@ 2u2af-1p -1mw. (3-110)
На рис. 3.19 приведены построенные частотные характеристики для рассматриваемого примера. Они свидетельствуют, что при некоторых частотах колебаний движения ведущего конца каната (колебаний скорости вращения тянущего электродвигателя) или колебаний сил сопротивления возможно такое явление, как субгармонический резонанс.
Пример 3.7. Описать колебания напряжений в узле крепления теплообменной трубы (рис.3.20). Заделка трубы в доске трубной выполнена с помощью роликовых вальцовок.
При решении такой задачи применим выше описанные методы[11] .
Интенсивность распределенной нагрузки q= const. Кроме этого в пролете трубы действует переменная сила F. Оба воздействия обусловлены проходящими потоками жидкости

Рис. 3.20
Схема закрепления трубы
Возможными реакциями опор являются: D, В и момент в заделке M0.
Задача - статически неопределимая. Составим уравнения равновесия:
B+ D= F+ qL2/2; B(a+c) + M0= Fc. (3-111)
Реакцию опоры В определим с помощью теоремы Кастильяно, положив прогиб в точке В, равным нулю, т.е.
yB=0= ¶ U/¶ B= (EJ)-1{ 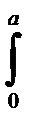 M1 (¶ M1/ ¶ B) dx+
M1 (¶ M1/ ¶ B) dx+ 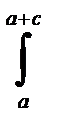 M2 (¶ M2/ ¶ B) dx} , (3-112)
M2 (¶ M2/ ¶ B) dx} , (3-112)
где U= M2/ (2EJ)- потенциальная энергия изогнутой балки.
Изгибающие моменты на 1-м и 2-м участках M1 , M2 определяются уравнениями M1=Bx- qx2/2 ; M2= Bx – qx2/2- F(x-a).
Следовательно,
¶ M1/¶ B= x; ¶ M2/¶ B = x.
Подставим эти соотношения в (3-112)
0= 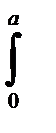 ( Bx- qx2/2)xdx+
( Bx- qx2/2)xdx+ 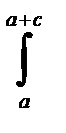 [ Bx – qx2/2- F(x-a)]xdx=
[ Bx – qx2/2- F(x-a)]xdx=
= (Bx3/3- qx4/8)  + [Bx3/3- qx4/8- F(x3/3- ax2/2 )]
+ [Bx3/3- qx4/8- F(x3/3- ax2/2 )]  =
=
= B- q(a+c)/8- F{1+a3/[2(a+c)3]-3a/[2(a+c)]}.
Откуда
B= q(a+c)/8+ F{1+a3/[2(a+c)3]-3a/[2(a+c)]}. (3-113)
Таким образом, уравнения моментов можно записать в форме
M1=FZx- qx2/2; M2= FZx- qx2/2- F(x-a)= Fx(Z-1)+ Fa- qx2/2, (3-114)
где Z= 1+a3/[2(a+c)3]-3a/[2(a+c)].
Для определения прогиба в точке приложения силы используем теорему Кастильяно, т.е.
yА= ¶ U/¶ F= (EJ)-1{(EJ)-1{ 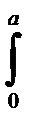 M1 ¶ M1/ ¶ F dx+
M1 ¶ M1/ ¶ F dx+ 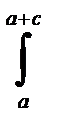 M2 ¶ M2/ ¶ F dx, }
M2 ¶ M2/ ¶ F dx, }
Учитывая (3-114), получим ¶ M1/¶ F=Zx ; ¶ M2/¶ F=[(Z-1)x+a] .
После подстановки этих соотношений в подинтегральные функции, получим прогиб в точке A
yA= -JF F - Jq q , (3-115)
где JF = {Z2a3/3+ (Z-1)2[(a+c)3- a3]/3+ ca2+ (Z-1)a[(a+c)2- a2]}/(EJ);
Jq = Za4/8+ (Z-1)[(a+c)4- a4]/8+ a[(a+c)3- a3]/6 - коэффициенты упругости.
Положим, что
F(t) = F0(t)+ hAu(t)+ mцт du/dt, (3-116)
где mцт = rf(a+c)- масса пролета трубы, сосредоточенная в центре пролета трубы точке А; hA - коэффициент потерь, приведенных к центру пролета, на трение; u - скорость поперечного движения центра пролета.
Тогда после дифференцирования (3-115) по времени, получим
u(t)=- JF pF(t).
а с учетом (3-116)-
u(t)=- JF p[F0(t)+ hAu(t)+ mцт pu(t)]
или
u(t)(1+ hAJF p+ mцтJF p2)= - JF pF0(t). (3-117)
Можно показать, что это уравнение системы с сосредоточенными параметрами, несмотря на распределенность нагрузки по длине пролета, дает весьма точное значение 1-й резонансной частоты. Поскольку многие реальные динамические параметры определяются низкими, наиболее энергонасыщенными частотами, то уравнение (3-117) можно использовать при динамическом анализе.
Определим колебания нормальных напряжений в заделке.
Запишем уравнение моментов для этого сечения
M0(t)=F(t)c- B(a+c)= F(t)c- q(a+c)2/8- F(a+c)Z}= F(t)[c-(a+c)Z]- q(a+c)2/8 .
Подставим сюда (3-116)
M0(t)=[c- (a+c)Z][F0(t)+ hAu(t)+ mцт pu(t)]- q(a+c)2/8. (3-118)
Тогда напряжение в заделке равно sо(t)= M0(t)/Wz, где Wz - геометрический момент сопротивления сечения трубы.
Колебания напряжения можно описать с помощью уравнения
Dsо(t)=W-1z [c- (a+c)Z][F0(t)+ hA u(t)(1+ T2 p)],
где Т2= mцт/ hA.
После подстановки в это выражение (3-117), получим
Dsо(t)=W-1z [c- (a+c)Z]F0(t)/ (1+ hAJF p+ mцтJF p2). (3-119)
Резонансная частота
wрез= 1/(mцтJF)1/2 . (3-120)
Дата добавления: 2015-02-23; просмотров: 1201;
