Динамика и статика стержней и стержневых систем

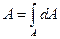
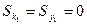
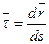
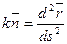
Представим себе, что в пространстве задана кривая уравнением 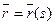и следовательно в каждой ее точке определен подвижный трехгранник. Будем считать, что задана плоская фигура и для нее определен центр тяжести и главные центральные оси инерции. Выберем на кривой начало отсчета точки О, совместим ее с центром тяжести фигуры и повернем фигуру так, чтобы один из главных векторов центр осей инерции была направлена вдоль нормали, а вторая вдоль бинормали. Тогда касательная к кривой перпендикулярна плоской фигуре. В дальнейшем расположенную плоскую фигуру будем называть поперечным сечением. Перемещая плоскую фигуру вдоль кривой так, чтобы описанное положение главных осей инерции не изменялось, получим объем ограниченным начальным и конечным положением фигуры (торцами) и поверхность который замыкает контур С.

Если заполнить этот объем деформируемой средой, то полученное тело называется стержнем.

По умолчанию предполагаем, что расстояния между торцами отсчитанное вдоль образующей превосходит наибольший размер поперечного сечения.

Будем считать, что внутри стержня изменение физико-механических характеристик (плотности, модули упругости и т.д.) определяется гладкими и непрерывными функциями координат. Тоже самое можно сказать и о фигуре поперечного сечения.

Если имеются нерегулярности в физико-механических или геометрических свойствах, то такой объект будем называть стержневой системой.

Классификация стержней осуществляется по следующим признакам:

1. Вид оси стержня: прямые, плоские криволинейные, пространственные, естественно закрученные.

2. Изменение геометрических и физических характеристик вдоль оси: однородные, когда все постоянно; неоднородные, когда хотя бы что-нибудь меняется.

3. Форма поперечного сечения: круглое, квадратное и т.д.

4. Соотношение размеров: если длина стержня имеет порядок более 10 наибольших размеров поперечного сечения и, если аналогичные соотношение существует между наименьшим радиусом кривизны и характерным поперечным размером, то стержень называется тонким; если упомянутые соотношения имеют порядок единица, то стержень называется толстым; все остальные стержни – средней толщины.