Кинематика деформированных стержней
Деформирование стержней связно с движением поперечного сечения совместно с осью.
Деформирование стержней рассматривается на основании кинематической гипотезы Бернулли: поперечное сечение в деформированном состоянии располагается по отношению деформированной оси стержня, также как и до деформации и не изменяет поперечных размеров.
 | |||
 | |||
|
|
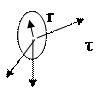
Рис. 1
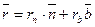
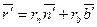
Кинематическая гипотеза Бернулли исключает из рассмотрения эффект Пуассона, т. е. уменьшения поперечного сечения при одноосном растяжении стержня. Это является одним из источников подвижности теории стержней, основанное на гипотезе Бернулли.
Подвижность этой теории имеет порядок: 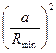
В соответствии с принятой гипотезой деформирование стержня можно рассматривать как следствие относительного движения двух близко расположенных поперечных сечений. Допустим, что одно из сечений неподвижно. Если второе поперечное сечение перемещается относительно  одного таким образом, что нормаль к поперечному сечению всегда совпадает с вектором
одного таким образом, что нормаль к поперечному сечению всегда совпадает с вектором 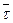 недеформированной оси, то говорят, что стержень находится в состоянии растяжения/сжатия.
недеформированной оси, то говорят, что стержень находится в состоянии растяжения/сжатия.
При таком виде напряжения деформированного состояния отсутствуют деформации сдвига, а деформация растяжения / сжатия любые волокна эквидистантного оси стержня не зависит от длины радиус – вектора 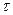 (рис. 1)
(рис. 1)
Если второе поперечное сечение поворачивается в пространстве относительного вектора 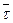 , причем
, причем 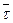 не меняет своего направления, то такое напряженное деформированное состояние называется кручением.
не меняет своего направления, то такое напряженное деформированное состояние называется кручением.
При рассмотрении кручения пренебрегают удлинением волокна, связанным с его поворотом (эффекта Пойнтинга). Такое допустимо только при малых углах относительного поворота.
Если при деформировании поперечное сечение поворачивается относительно единичных векторов 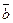 и
и 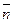 , то говорят, что стержень находится в состоянии изгиба.
, то говорят, что стержень находится в состоянии изгиба.
Если второе поперечное сечение перемещается по направлению нормали или бинормали и при этом не поворачивается, то такое напряжение деформированного состояния называется сдвигом.
В дальнейшем при рассмотрении различных напряжений деформированного состояния будем считать перемещение оси стержня малыми, имеющими порядок половины наименьшего размера поперечного сечения, угловые перемещения также будем считать малыми в смысле:
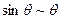
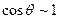
Дата добавления: 2015-02-16; просмотров: 1123;
