Динамики стержней

Для прямого стержня с постоянным сечением применять МКЭ не стоит, как и в задачах статики. МКЭ оказывается эффективным для неоднородных стержней и стержневых систем. Пока рассмотрим такую стержневую систему, у которой все ее элементы есть прямые стержни постоянного сечения. Для того, чтобы сформулировать матричные соотношения для одного конечного элемента добавим в вариационный функционал Лагранжа силы инерции и найдем их виртуальную работу:

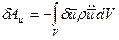
Будем считать, что в этом выражении 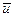есть перемещение некоторой точки, которая определяется обычной конечно-элементной формулой:

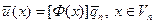
где координата х есть локальное координата конечного элемента с номером n, 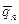- вектор узловых перемещений этого элемента, 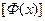- матрица функции формы.

Как и ранее будем считать, что инерция поворота поперечного сечения пренебрежимо мала по сравнению с инерцией поступательного перемещения. Тогда для виртуальной работы сил инерции:

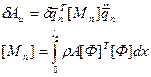(2.112)

Матрица М является матричной характеристикой конечного элемента и называется матрицей масс. Тогда для одного конечного элемента можно сформулировать выражение вариационного принципа Лагранжа.

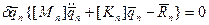(2.113)

Если на конечный элемент не наложено никаких кинематических ограничений, то из (2.113) получается система уравнений движения конечного элемента.

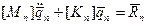(2.114)

Система (2.114) может быть решена, если заданы начальные условия (начальные узловые перемещения и начальные узловые скорости). Результат решения представляет собой законы движения узлов в пространстве. При этом результат решения представляет собой наложение движений, связанных с деформацией стержня на его движение как абсолютно твердого тела.

В дальнейшем будем считать, что на стержневую систему наложены кинематические ограничения, обеспечивающие отсутствие движения системы как абсолютно твердого тела. Кроме того, будем считать, что углы поворота стержней, связанные с деформированием, являются малыми в том смысле, что их квадратами можно пренебречь по сравнению с первой степенью и считать синусы равными самим углам, а косинусы равными 1.

Данное предположение позволяет считать локальную координатную систему конечного элемента неподвижной, тем самым из математической модели исключаются уравнения относительного движения локальной системы.

Переход к ансамблю конечных элементов осуществляется также как в статике. Матрица масс ансамбля конечных элементов получается с помощью того же алгоритма, что и для матрицы жесткости в этом не трудно убедиться, если в (2.113) перейти от локальных к глобальным координатам и затем просуммировать выражения принципа Лагранжа для всех конечных элементов.

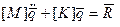
где [М], [К] – матрицы масс и жесткости соответственно, 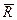- вектор нагрузок.