Спектр продольных, крутильных и поперечных колебаний
Раннее было замечено, что задача растяжения/сжатия и кручения приводится к одноименным дифференциальным уравнениям. Общий вид этих уравнений в случае задачи о свободных колебаниях следующий:
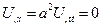
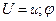
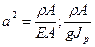
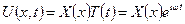
Подставляем:
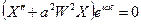
Потребуем, чтобы: 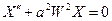
Решение этого уравнения:
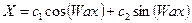 (2.94)
(2.94)
Полученные формы колебаний должны удовлетворять краевым условиям в перемещениях (однородных).
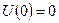 - перемещение равно нулю
- перемещение равно нулю
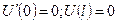 или
или 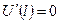
Запишем соответствующую систему алгебраических уравнений. Характеристические уравнения выводятся из краевых условий. Например, стержень, защемленный одним концом и свободный на другом конце.



 U
U
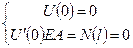 - продольная сила
- продольная сила
Показанные краевые условия относятся к функции 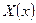
Т.к. они должны выполнятся при любом законе движения 
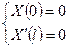
Тогда 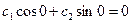
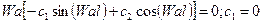
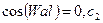 - произвольная характеристика уравнения
- произвольная характеристика уравнения
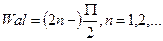
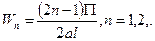
Последнее выражение – спектр свободных колебаний для данной расчетной схемы. Формы свободных колебаний определяются выражением:
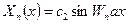
Т.к. постоянное 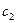 произвольное, определим ее из условия нормирования.
произвольное, определим ее из условия нормирования.
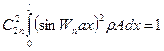
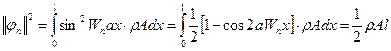
Формы свободных колебаний:

После определения форм свободных колебаний нетрудно найти коэффициенты разложения уравнения (2.88).
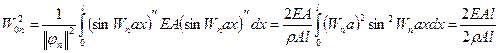

Задача о свободных колебаниях прямых стержней.
Для решения задач о свободных колебаниях, заметим, что все уравнения состояния (при растяжении, кручении и изгибе) содержит производную только четных порядков. Из теории дифференциальных уравнений математической физики известно, что зависимость от времени решений таких уравнений представляет собой гармоническую функцию вида:
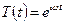
Подстановка такой зависимости в уравнение состояния приводит к обыкновенному дифференциальному уравнению относительно зависимости перемещения от продольной координаты. Так как уравнение состояния при отсутствии распределенной нагрузки является однородным. То решением последнего уравнения называют форму или формы свободных колебаний. Они являются функциональным базисом для представления движения произвольной точки стержня как при возмущении начальными скоростями и перемещениями, так и при возмущении нагрузкой.
Так как собственная форма есть собственная функция линейного дифференциального оператора, то они обладают свойствами ортогональности и полноты (теорема Стеклова). Полученные аналитические выражения для форм свободных колебаний для простейших напряженно-деформированных состояний.
1. Растяжение/сжатие и кручение.
Уравнение состояния для растяжения/сжатия и кручения имеет следующий вид:
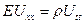
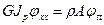
Предполагается, что стержень однородный в следующем смысле:
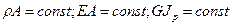
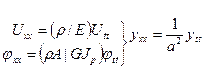
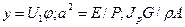
Перейдем в этом уравнении к безразмерной координате:
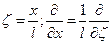
Тогда уравнение примет вид:
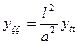
Подставим функцию: 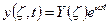
 (2.95)
(2.95)
Последнее уравнение определяет формы свободных продольных и крутильных колебаний. Решение уравнения с помощью универсальной подстановки имеет вид:
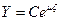
имеем из (2.95) характеристическое уравнение:

Таким образом, формы свободных колебаний при растяжении или кручении имеют вид:
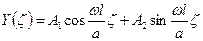
Параметр 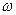 определяется из краевых условий, которые предполагаются однородными.
определяется из краевых условий, которые предполагаются однородными.
Возможны варианты:

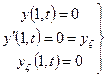 (2.97)
(2.97)
Записывая систему уравнений, отметим, что в любом из трех случаев эта система будет однородной и для существования ее нетривиального решения следует считать главный определитель равным нулю. Это условие позволяет найти счетное множество значений параметра 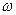 . В качестве примера рассмотрим определение форм свободных колебаний для стержня , защемленного двумя концами.
. В качестве примера рассмотрим определение форм свободных колебаний для стержня , защемленного двумя концами.
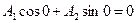
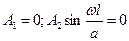
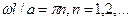 (2.98)
(2.98)
 (2.99)
(2.99)
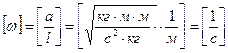
Параметр 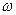 , имеющий размерность
, имеющий размерность 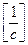 имеет физический смысл частоты свободных колебаний стержня, множество его значений называется спектром колебаний.
имеет физический смысл частоты свободных колебаний стержня, множество его значений называется спектром колебаний.
1.) Для растяжения стержня:
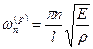 (2.100)
(2.100)
2.) Для кручения:
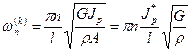 (2.101)
(2.101)
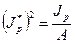 - полярный радиус стержня
- полярный радиус стержня
Для защемленного стержня свободное движение можно представить в виде:
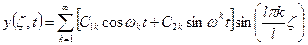 (2.102)
(2.102)
Постоянные 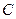 определяются из начальных условий. Они представляют собой коэффициенты разложения в ряд Фурье по формам свободных колебаний зависимостей начального перемещения и начальной скорости от продольной координаты. Для рассмотренного случая это разложение есть ряд Фурье по
определяются из начальных условий. Они представляют собой коэффициенты разложения в ряд Фурье по формам свободных колебаний зависимостей начального перемещения и начальной скорости от продольной координаты. Для рассмотренного случая это разложение есть ряд Фурье по 

Из (2.102) имеем:
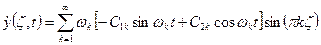 (2.103)
(2.103)
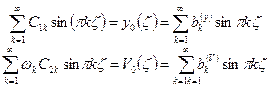
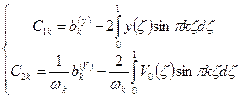
2. Плоский поперечный изгиб.
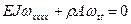
Приведем уравнение к безразмерному виду:
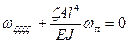
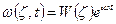
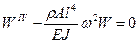 (2.104)
(2.104)
Это уравнение описывает формы свободного колебания.
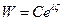
Характеристическое уравнение примет вид:
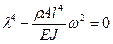
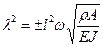
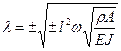
 принимает два вещественных и два мнимых значения, общее решение (2.104) представимо в виде.
принимает два вещественных и два мнимых значения, общее решение (2.104) представимо в виде.
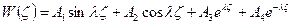 (2.105)
(2.105)
На основании (2.105) можно сформировать систему краевых условий и найти 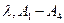
Крыловым была предложена иная форма записи общего решения, позволяющая сразу найти два из четырех произвольных постоянных 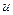 и тем самым понизить порядок системы краевых условий до второго порядка. Им были введены так называемые балочные функции или функции Крылова.
и тем самым понизить порядок системы краевых условий до второго порядка. Им были введены так называемые балочные функции или функции Крылова.
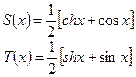 (2.106)
(2.106)

Эти функции отличаются следующим:
1.)правилом циклического дифференцирования, то есть:
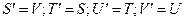
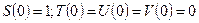
Указанное свойство функции Крылова позволяет записать выражение для форм свободных колебаний в виде:
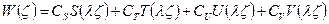 (2.107)
(2.107)
и его производных, включая третью:
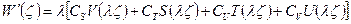 (2.108)
(2.108)
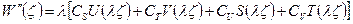 (2.109)
(2.109)
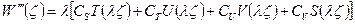 (2.110)
(2.110)
Все постоянные определяются из краевых условий. На каждом краю стержня могут быть заданы следующие комбинации кинематических и силовых факторов.





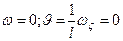














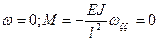
 |  |




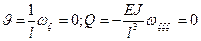

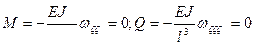
Рассмотрим пример определения форм свободных колебаний для шарнирно-опертого стержня.
Краевые условия для этого стержня:
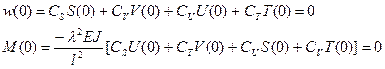
Из первого уравнения: 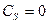
Из второго уравнения: 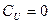
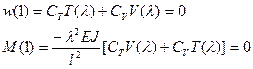
Последняя система уравнений однородная, она имеет решение при условии равенства 0 ее определителя.
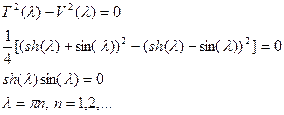
Полученные значения  позволяют записать выражение для спектра свободных поперечных колебаний.
позволяют записать выражение для спектра свободных поперечных колебаний.
 (2.111)
(2.111)
Полученный результат единственный, в котором удается найти аналитическое выражение для спектра. Во всех остальных случаях характеристическое выражение содержит различные комбинации тригонометрических и гиперболических функций, которые не удается привести к тригонометрическому уравнению. В частности для стержня, защемленного одним концом с другим свободным концом, это уравнение имеет вид:
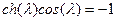
Т.к. гиперболические функции быстро возрастают при возрастании  , то при численном решении характеристического уравнения полезно поделить его правую и левую часть на
, то при численном решении характеристического уравнения полезно поделить его правую и левую часть на  . Опыт показывает, что в этом случае легко отделяются корни и удается показать асимптотическое выражение для корней с большими n.
. Опыт показывает, что в этом случае легко отделяются корни и удается показать асимптотическое выражение для корней с большими n.

После определения спектра колебаний следует построить выражение для собственных форм. Для этого запишем систему алгебраических уравнений относительно 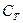 и
и 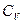 для фиксированного номера собственной частоты.
для фиксированного номера собственной частоты.
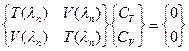
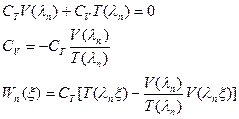
Проделывая преобразование последнего выражения, можно получить:
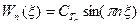
Теперь движение произвольное точки изгибаемого стержня при свободных колебаниях можно представить в виде:
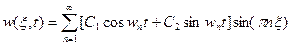

Замечание: в рассмотренном ранее методе модального разложения требуется, чтобы формы свободных колебаний были ортонормированны в смысле:
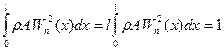
Используя последнее выражение для 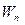 получим:
получим:
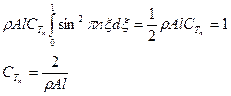
Таким образом, мы имеем возможность строить формы свободных колебаний при простых напряженно-деформированных состояниях и определять спектры свободных колебаний. Полученные результаты используются для определения реакций стержня на произвольное внешнее воздействие с помощью метода модального разложения (см. выше).
Примеры решения задач о свободных и вынужденных
движениях стержня.
Задача 1.

Найти спектр колебаний данного стержня.
Решение:
Записываем функции Крылова:
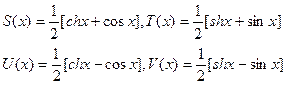
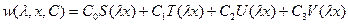 - прогиб
- прогиб
 - угол поворота
- угол поворота
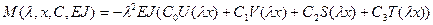 - момент
- момент
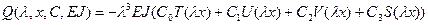 - перерезывающая сила
- перерезывающая сила
Составляем характеристическое уравнение.
Из граничных условий на левом краю имеем:
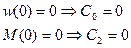
Из граничных условий на правом краю имеем:
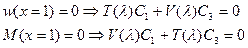
Получили однородную систему.

правая часть характеристического уравнения
частоты свободных колебаний
Определение постоянных. Для определения постоянных 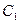 ,
, 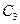 решаем однородную систему уравнений (r=1).Удаляем из системы первую строку и выражаем
решаем однородную систему уравнений (r=1).Удаляем из системы первую строку и выражаем 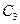 через
через 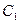 :
:

Подставляем значения постоянных в выражение для перемещения получаем:
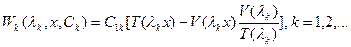
Найдем параметр 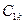 из условия нормирования:
из условия нормирования:
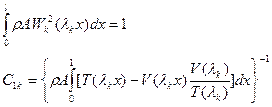
Полученные формы свободных колебаний используются для описания свободных и вынужденных движений при произвольных внешних воздействиях.
Задача 2.
Найти реакцию стержня задачи 1 на возмущение начальной скоростью по закону:
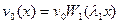
Решение:
Предполагается, что спектр свободных колебаний (формы и частоты) известен.
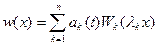
Интеграл Дюамеля:
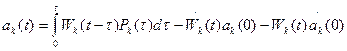
Т.к. отсутствуют внешние нагрузки, то 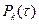 =0, отсутствуют начальные перемещения
=0, отсутствуют начальные перемещения 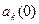 =0.
=0.
Импульсно-переходная характеристика:
 .
.
Для определения движения любой точки необходимо найти параметры 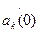 .
.

Задача 3.
Найти реакцию стержня задачи 1 при однородных начальных условиях на равномерно распределенную по длине нагрузку, изменяющуюся со временем по закону прямоугольного импульса:
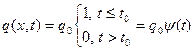


Решение:

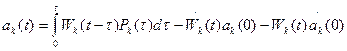
Начальные условия однородны: 
Параметры 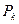 находим, записывая разложение внешней нагрузки по модам колебаний.
находим, записывая разложение внешней нагрузки по модам колебаний.
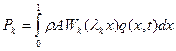
Представим 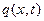 в виде
в виде 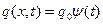
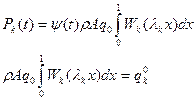
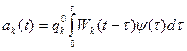
1) 
 :
:
Дата добавления: 2015-02-16; просмотров: 1394;
