Классификация задач динамики

Все разрешающие уравнения динамики стержней относятся к уравнениям математической физики и методы решения их известны.

Будем классифицировать задачи динамики следующим образом:

- если силовые воздействия (распределенные и сосредоточенные силы и моменты) отсутствуют, то деформации могут происходить только за счет неоднородных начальных условий. Такие задачи называются задачами о свободных колебаниях.

- если начальные условия распространяются не на всю длину стержня, а локализовано на некотором отрезке длиной 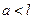, то можно поставить и решить волновую задачу.

- если задача неоднородна, т.е. влияние нагрузки отлично от нуля и является известными функциями времени, то такие задачи называют задачами о вынужденных колебаниях и в этом случае, если нагрузки локальны, то можно ставить и решать задачи распространения волн.

Для решения задач всех классов будем использовать одну из возможных форм метода Фурье, т.к. волновые решения получаются из метода Фурье элементарными преобразованиями.

Все уравнения состояния стержней относятся к линейным дифференциальным уравнениям, а при постоянной жесткости и массе 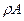к линейным уравнениям с постоянными коэффициентами.

Для такого рода линейных операторов можно поставить задачу Штурма-Лиувилля по определению собственных чисел и собственных функций этого оператора.

В курсе уравнений математической физики рассматривались методы Стеклова, утверждающие, что собственные функции линейных операторов образуют полную ортогональную систему функций. Следовательно решение любой задачи динамики может быть представлено в виде суммы сходящегося ряда.

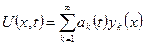,где

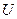- искомое перемещение;

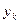- собственные функции линейного оператора уравнения состояния;

- коэффициенты, подлежащие определению через известные внешние нагрузки и начальные условия.

Если решена задача Штурма-Лиувилля, то функция 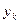известна.

Подстановка последнего выражения в вариационное уравнение Лагранжа приводит к системе обыкновенных дифференциальных уравнений относительно коэффициентов .

Эта система уравнений второго порядка имеет диагональную матрицу в силу ортогональности собственных форм операторов.

В общем виде уравнения этой системы выглядят так:

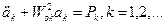(2.88)

где

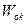-собственные числа линейного оператора

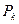-представляют собой коэффициенты разложения внешней распределенной нагрузки по базису 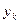, а собственные функции предполагаются нормированными в смысле

(2.89)

Уравнение (2.88) универсально по отношение к виду напряженно-деформированного состояния и поэтому решение задач динамики можно разделить на две части:

1) определение функционального базиса из решений задачи Штурма-Лиувилля для линейного оператора, соответствующего виду напряженно-деформированного состояния

2) решение уравнения (2.88) для определения коэффициентов разложения

После этого выражение для перемещений определяется формулой (2.87); напряжения и деформации определяются дифференцированием (2.87) и домножением на модуль упругости.

Рассмотрим метод решения уравнения (2.88).

Для решения уравнений вычислим интегральное преобразование Фурье от правой и левой части (2.88); индекс k опустим для сокращения записи.

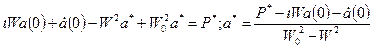- решение в изображении

Перейдем к оригиналу введя обозначения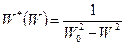

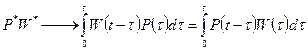- теорема о свертке

- теорема дифференцирования оригинала

Аналитическая форма:

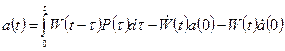интеграл Дюамеля (2.90)

Функция 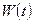называется импульсно-переходной характеристикой.

Т.к. уравнение (2.90) формулируется для каждого собственного числа оператора, то стержень имеет счетное множество импульсно-переходных характеристик, которые образуют диагональную матрицу.

Оригинал импульсно-переходной характеристики

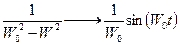
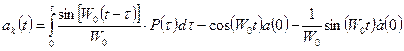
Формулы (2.87), (2.91) – (2.93) дают аналитическое решение задачи динамики, если известны базисные функции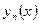

Это решение включает в себя все рассмотренные классы задач динамики. При Р=0 (2.91) дает решение зада о свободных колебаниях; в зависимости от начальных условий, что отражают формулы (2.93), можно получить решение волновой задачи. При 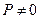и однородных начальных условиях можно получить решение задачи для любого закона изменения внешней нагрузки по времени и любого ее распределения по координате. Т.к. рад (2.87) сходящийся. То можно считать, что полученное решение является точным. При конкретных вычислениях ограничиваются конечным числом членов ряда, допускаемая при этом погрешность может быть оценена по абсолютной величине последнего оставшегося члена. Если считать, что норма внешней нагрузки ограничена, то оценка погрешности имеет вид:

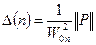
Здесь n – последнего оставшегося члена ряда.