В моделировании пластин и оболочек

Основная кинематическая гипотеза при моделировании оболочек или гипотеза прямой нормали (Кирхгоф-Ляв) звучит следующим образом: материальное волокно, нормальное к срединной поверхности оболочки в недеформированном состоянии после деформации остается нормальным к деформированной поверхности и не изменяет своей длины. Как и в теории стержней, следствием этой гипотезы является линейное распределение перемещений по толщине оболочки.

Статистическая гипотеза в теории оболочек формулируется почти также как в теории стержней: слои, параллельные срединной поверхности, не надавливают друг на друга. Тем самым компоненты тензора напряжений, имеющие индекс 3 равны 0.

Следствием обеих гипотез является то, что слои, параллельные срединной поверхности, находятся в плоском напряженном состоянии. Будем считать, что материал оболочки линейно-упругий и деформации малы, т.е. квадраты углов поворота нормального волокна пренебрежимо малы по сравнению с их первыми степенями.

Принятые кинематические гипотезы позволяют рассматривать деформацию в срединной поверхности как основную, а деформацию любого слоя получать по известным перемещениям точек срединной поверхности. Пусть на поверхности заданы криволинейные координаты 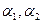так, что в любой точке поверхности определены два базисных вектора:

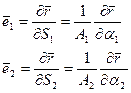(2.124)

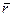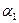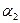где - радиус-вектор срединной поверхности, определенный как функция криволинейных координат и . Параметры 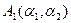, 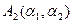- параметры Ляме, которые определяют связь между элементом длины дуги и дифференциалами криволинейных координат.

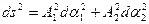
Выбор криволинейных координат обусловлен одним из признаков классификации оболочек, а именно формой срединной поверхности, например, если срединная поверхность есть плоскость, то в качестве координат 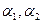удобно принять декартовы оси x, y, лежащие в срединной плоскости.

1) пластинка:

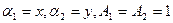
2) цилиндрическая замкнутая оболочка:

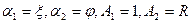
где 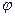- полярные угол, 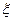- меридианная координата (длина меридиана – длина образующей), R – радиус срединной поверхности.

3) сферическая оболочка:

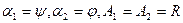
где 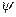- широта, 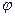- долгота.

4) коническая оболочка:

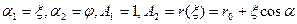
где 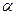- угол полураствора конуса.

5) торроидная оболочка.

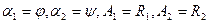
В общем случае базисные векторы 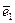, , 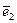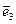выбираются таким образом, чтобы 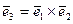и направление 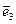совпадало бы с направлением к центру кривизны.

Данное требование – выбор внутренней нормали не является обязательным. В литературе по оболочкам встречаются как 1-ый, так и 2-ый варианты.

Очевидно, что при перемещении точки по срединной поверхности базисные векторы 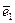, , 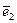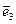в общем случае поворачиваются и потому при вычислении компонент тензора деформации этот поворот также учитывается, что существенно усложняет расчетные формулы теории оболочек в общем случае.

Будем рассматривать различные варианты оболочек, последовательно начиная с самого простого, когда срединная поверхность есть плоскость.