Горизонтальная пластина

Как следует из формул (7.21),кривая Z имеет пять точек экстремальных значений. По оценке получим

Z(х=0) = ;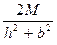

;

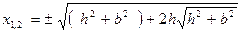(8.7)

.

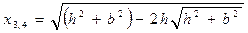Точки х_1,2 соответствуют Z_min, а точки х_3,4 имеют реальное значение при условии b > h 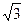; в этом случае в точках х₃ и х₄, находящихся почти над краями горизонтального пласта, возникают максимумы Z (рис.7.11). С увеличением горизонтальной мощности пласта значение Z(0) над его центром убывает. Кривая Z пересекает ось х в точках х_5,6 = . Объединив представленные уравнения, получаем формулу для оценки глубины залегания горизонтальной пластины (пласта):

.

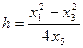Если имеется кривая Н, то по аналогии можно найти связимежду ее характерными точками и элементами залегания пласта.

8.3. Метод касательных

Методы касательных основаны на аналитической зависимости ряда характерных точек кривой от параметров возмущающих объектов. В качестве основной исходной точки выбирают точку перегиба кривой исходного поля. Поэтому зависимость между координатами этой точки и параметрами возмущающих объектов выражается не через исходное поле, а через его производную в этой точке. В качестве дополнительных точек для составления системы уравнений выбираются любые другие точки: максимального и минимального значения поля, половины максимального значения; точки, где касательные к графику имеют наклон в два раза меньше, чем наклон основной касательной. Формулы для расчета глубин намагниченных объектов получаются из системы уравнений касательных, проведенных к точке перегиба и к какой-либо другой точке. Для каждой конкретной модели эти формулы будут иметь свои зависимости и могут быть использованы только для этого класса моделей.

Способ касательных является эвристическим, т.е. получен без учета теории магниторазведки. Геофизик Ю.H. Грачев на примере аномальных графиков над шаром и круговым цилиндром по расстояниям между точками пересечения касательных, проведенных к характерным точкам заданной функции, нашел возможность определять глубину до поверхности (не до центра) магнитного источника.

На рис.8.5 A₁A₂ ‑ касательная в точке максимума, В₁В₂ и В₃В₄ – касательные в точках минимумов и C₁C₂ и C₃C₄ ‑ касательные в точках перегиба. Обозначая х₁, х₂, х₃ и х₄ ‑ абсциссы точек пересечения касательных, по разностям х₂–х₁ и х₄–х₃ предлагается находить глубину по следующей формуле:

h = 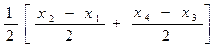. (8.8)

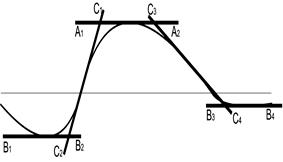
Рис.8.5. К определению глубины залегания

магнитного тела способом касательных

За рубежом этот метод называют методом наклона, так как он использует величину горизонтального градиента или наклон графика аномалии в точке перегиба. Метод основан на эмпирических наблюдениях, по данным которых установлен множитель К, являющийся коэффициентом пропорциональности между искомой глубиной и горизонтальным отрезком по оси Х =L, отсекаемым касательными.

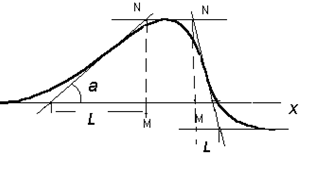
По графику аномальной кривой проводят касательные в точке положительного и отрицательного экстремума и в точке максимального градиента, т.е. в точке перегиба кривой (рис. 8.6). Полученная длина отрезка L в масштабе графика является функцией глубины и формы тела.

Рис.8.6. Модификации метода касательных

По изменению графика представим

L = MN / tg 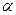, (8.9)

где MN – наибольшая амплитуда, а 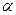– наибольший угол наклона кривой. Величина tg a численно будет равна первой производной исследуемой кривой в точке перегиба.

Таблица 8.1

Значения глубины тела h в долях отрезка L, т. е. величины h : L для различных форм тел, приводятся в табл. 8.1.

Рассмотрим практические методы определения глубины залегания некоторых тел.