Тонкий пласт, ограниченный по глубине

При небольшой протяженности вертикально намагниченного пласта по глубине нижний край пласта, отрицательно намагниченный, будет оказывать заметное влияние на вид магнитной аномалии, форма кривых Z и Н будет несколько изменяться. В периферийных частях четкой положительной аномалии Z будут появляться слабые отрицательные поля (рис.8.4).

Для пласта небольшой мощности будем иметь

,

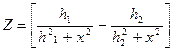над центром пласта получим

,

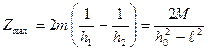где m = 2 bl, M – магнитный момент сечения пласта, M = 2 b J 2 l = J S.

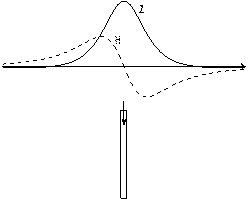
Рис. 8.4. Магнитное поле тонкого пласта, ограниченного по глубине

В этом случае определяется глубина залегания центра пласта h₀, площадь сечения S, половина вертикальной длины l и глубина до верхнего края пласта h₁:

h₁ = 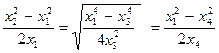, (8.4)

где х₁ – расстояние от центра аномалии до точки, где Z = 0, х₂ – расстояние от центра аномалиидо минимума Z_min , х₃ – расстояние от центра аномалии до точки, где Z = 0,5 Z_max , х₄ – расстояние от центра аномалии до пересечения Z и H.

8.2.5. Мощный пласт

В случае мощного вертикально падающего пласта на симметричном аномальном графике Zа находят точки x_1/2 и x_1/4, в которых значения аномалий в 2 и 4 раза меньше, чем в начале координат. Для вычисления h и b используются формулы

,

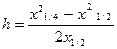(8.5)

.

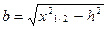Для определения J используется значение Za при х=0. В случае наклонного двухмерного пласта шириной 2в, намагниченного вертикально и бесконечно погруженного в глубину, согласно формулам (7.19, 7.20), кривые Z и Н имеют асимметричный вид. Графики могут быть разложены на составляющие в виде четной f(х) и нечетной φ(х) функций. Уравнение (7.19) перепишется в виде

Z=f(x)-φ(x).

Начало координат соответствует эпицентру верхней кромки пласта. Для определения местонахождения эпицентра используется тождество

Z (0) = / Z_max / - / Z_min /.

Далее по соотношениям (7.6) строятся четная и нечетная функции. Первая кривая f(х) с точностью до постоянного коэффициента соответствует кривой арктангенса:

f (x) = 2 J sin²α arctg .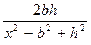

Положение характерных точек совпадает с кривой вертикальной составляющей над вертикальным пластом большой мощности. Определение элементов залегания его можно найти по формулам (8.3, 8.4).

Нечетная полученная новая кривая соответствует функции логарифма

φ (x) = J sinα cosα ln ,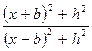

ее вид совпадает с кривой горизонтальной составляющей напряженности магнитного поля над мощным вертикальным пластом. Она используется совместно с f(х) для определения угла наклона пласта по отношению функций f(х)/φ(х) для любой точки x профиля:

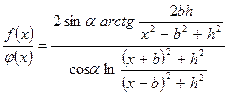. (8.6)

Интенсивность намагниченности J можно определить по максимальному значению четной функции. Описанные приемы разложения на две функции широко используются при решении обратной задачи по аномальным гафикам над контактами двух пород, сбросов и уступов.