Пластинки. Внутренние силовые факторы

Гипотеза прямых нормалей, уравнение Коши и закон Гука приводят к линейному по толщине распределению напряжений. Плоскому напряженному состоянию соответствует равномерное распределение напряжений по толщине, а изгибу – линейное симметричное относительно срединной плоскости.

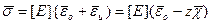
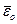- вектор деформации в плоском напряженном состоянии,

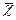- вектор кривизны,

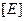- матрица постоянных упругости.

Введем внутренние силовые факторы, как главный вектор и главный момент нормальных и касательных напряжений, действующих в поперечном сечении пластинки. Компоненты главного вектора называются мембранными силами; они имеют размерность 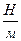и распределены по некоторым линиям, лежащим в срединной плоскости. Чаще всего используют мембранные силы, распределенные по координатным линиям. Компоненты этих сил образуют тензор 2 ранга и вычисляются по формулам:

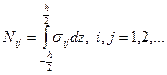(2.141)

Из предыдущего ясно, что мембранные силы при изгибе отсутствуют (для пластинки однородной по толщине). Тогда

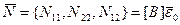(2.142)

Главные моменты напряжения определяются по общей формуле:

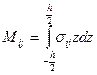(2.143)

Очевидно, что изгибающие моменты определяются только кривизнами и их выражение может быть записано в виде:

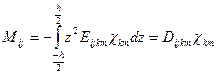(2.144)

Здесь

.

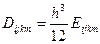Изотропное тело:

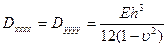- цилиндрические жесткости

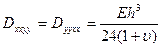
Момент 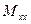стремится повернуть нормальное волокно относительно оси y, поэтому его называют изгибающим моментом. Принято считать положительным изгибающий момент, который стремится повернуть нормальное волокно против часовой стрелки, чему соответствует сжатие верхней части, и растяжение нижней части пластинки. На рис. показан отрицательный изгибающий момент 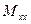. Аналогичное заключение можно сделать и для момента 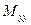. Момент 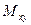поворачивает нормальное волокно таким образом, что оно не выходит из плоскости поперечного сечения, этот момент называется крутящим. Если нормальное волокно поворачивается против часовой стрелки при взгляде с направления внешней нормали к площадке, то условимся считать его положительным.

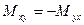
Из линейного распределения напряжений по толщине следует, что опасными могут быть точки либо верхней, либо нижней плоскости пластинки. Если материал имеет меньший предел прочности на растяжение, чем на сжатие, то опасными являются точки растянутой плоскости, если пределы прочности одинаковы, то опасная точка определяется наибольшим напряжением или в растянутой или в сжатой плоскости.

В связи с тем, что для разно сопротивляющихся материалов отсутствует единый подход к определению разрушительного напряжении, в дальнейшем примем, что пределы прочности (текучести) для материала пластинки одинаковы и предельные соотношения определяются энергетической теорией прочности.

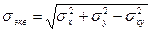(2.145)

и условие предельного состояния имеет вид:

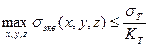(2.146)

Если пластинка находится в состоянии изгиба, то формулу (2.146) можно записать через внутренние силовые факторы, отличные от 0.

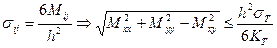(2.147)

Таким образом, для расчета пластинки на прочность достаточно построить распределение эквивалентных напряжений по верхней и нижней плоскости, выбрать точку с наибольшим эквивалентным напряжением и для этой точки проверить выполнение (2.146). Если пластинка находится в состоянии изгиба, то достаточно построить распределение эквивалентного момента по плоскости пластинки, выбрать точку с наибольшим эквивалентным моментом и проверить (2.147).