Основные соотношения для расчета упругих оболочек

Основные закономерности деформации оболочек, т.е. следствия из гипотезы прямых нормалей и статической гипотезы такие же, как и в теории пластинок, т.е. распределение напряжений по толщине оболочки также является линейным. В следствии этого в любом сечении плоскостью, проходящей через вектор нормали можно провести интегрированием по толщине и определить 3 мембранные силы 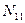, , 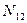, 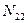два изгибающих момента 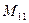и и 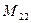крутящий момент 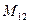. Здесь индексы 1, 2 указывают на криволинейную координату 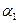или .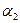

Особенностью, отличающей оболочку от пластинки, является то, что разделить состояние изгиба и плоское напряженное состояние срединной поверхностью не удается (по крайней мере, в общем случае). Причиной этого является поворот базисных векторов при движении по срединной поверхности оболочки.

Покажем возможности получения общих геометрических соотношений для оболочки произвольных ориентаций. Будем считать, что срединная поверхность определена параметрическими уравнениями 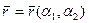, определены параметры 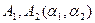, кривизны координатных линий .

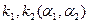Под 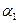и 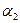понимаются криволинейные гауссовы координаты, которые получаются при пересечении поверхности с двумя перпендикулярными плоскостями, линия пересечения которых проходит через вектор нормали к срединной поверхности в данной точке и отличается тем, что кривизны линий пересечения в данной точке являются экстремальными (одна из них наибольшая, другая наименьшая).

Базисные векторы локальной координатной системы образуют подвижный трехгранник Дарбу.

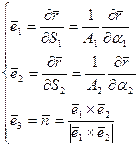(2.152)

Определим формулы дифференцирования базисных векторов.

Рассмотрим производные базисных векторов при движении по координатной линии 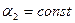. Будем рассматривать эту линию как пространственную кривую, для которой определен естественный трехгранник (трехгранник Френе). В этом трехграннике:

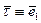- вектор касательной;

- вектор нормали;

- вектор бинормали.

Дифференцирование базисных векторов трехгранника Френе осуществляется по формулам Френе-Серре:

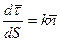
Здесь 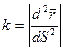- кривизна кривой;

- крутка (смешанное произведение трех векторов).

Для координатной линии .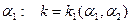

Производные по длине дуги 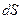вычисляется при 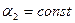и поэтому являются частными производными по длине дуги координатной линии 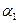, т.е.

,

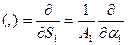тогда формулы Френе-Серре следует переписать так:

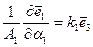
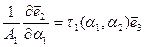(2.153)

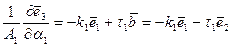
Рассуждая аналогично для линии , получим

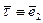- вектор касательной;

- вектор нормали;

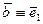- вектор бинормали.

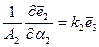
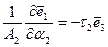(2.154)

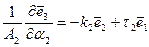
Рассмотрим деформацию срединной поверхности, при которой ее точки перемещаются в пространстве на вектор 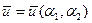, который представим разложением по подвижному базису

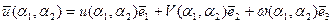
Сформулируем фундаментальное соотношение теории деформации

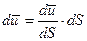
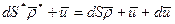
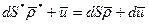
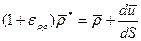
- относительное удлинение волокна в процессе деформации.

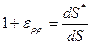
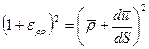
Особенности применения фундаментального соотношения теории деформации к деформации поверхности заключается в том, что деформирование проводится в криволинейной системе координат с подвижными базисными векторами. Градиенты перемещений нужно определять с учетом этого замечания.

Рассмотрим координатное волокно, определенное единичным вектором 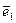. Из общего соотношения получим:

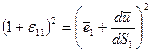
В данном случае градиент перемещения следует записать так:

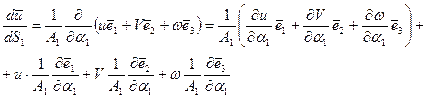
Приводя подобные члены при базисных векторах, получим:

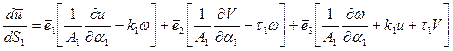- первый градиент перемещения.

Аналогичные формулы можно получить для производной вектора перемещения по координате 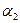. Затем, используя определение тензора деформации и пренебрегая квадратичными членами, получить выражение для компонент тензора малых деформаций. Таким образом определяются деформации срединной поверхности. Чтобы получить распределение деформаций по толщине, следует рассмотреть поверхность, которая отстоит от срединной на расстояние 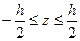. Все предыдущие выкладки сохраняются, но радиусы кривизны заменяются на величину .

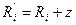Входящие в соотношение для деформации кривизны срединной поверхности

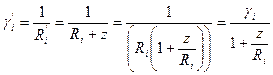
Для такой оболочки 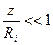, поэтому изменением кривизны при переходе от срединной поверхности к слою, отстоящему от нее на 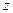, не сопровождается изменением кривизны, что упрощает соотношения для определения деформаций.

Общий вид компонент тензора деформаций для тонкой оболочки следующий:

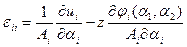
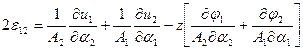
Здесь функци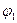и и 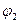- углы поворота нормали, которые вычисляются следующим образом:

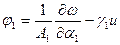
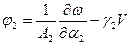
Из выражения для компонент тензора деформаций видно, что и в оболочках напряжение распределяется по толщине по линейному закону в том случае, если оболочка однородная по толщине и материал подчиняется закону Гука.

По аналогии с пластинками можно ввести внутренние силовые факторы: мембранные силы, изгибающие и крутящий моменты. Они вычисляются по тем же формулам, что и в теории пластинок.

Основное отличие теории пластинок от теории оболочек заключается в том, что в теории пластинок удается разделить плоское напряженное состояние и состояние изгиба и рассматривать их по отдельности. В теории оболочек уравнение проекций внутренних силовых факторов на направление подвижного трехгранника будут содержать мембранные силы и поправки второго порядка малости от поперечных сил.

В уравнения моментов с необходимостью войдут мембранные силы, т.к. вследствие конечной кривизны срединной поверхности мембранные силы даже при малых перемещениях дают момент относительно противолежащей им стороны элементарной площадки. Это означает, что задачи о плоской деформации и изгибе оболочки необходимо решать совместно. В следствии этой особенности уравнения в перемещениях, описывающие состояние оболочки в общем случае, являются весьма сложными. Их общее решение до сих пор не известно.

Аналитические решения задач теории оболочек в общей постановке найдены для простейших форм срединной поверхности (сфера, круговой цилиндр) и, как правило, содержит в себе ряд упрощающих предположений. Для реальных оболочек, имеющих сложную форму выреза, подкрепления и т.д., основным методом расчета является метод конечных элементов. Общие принципы построения функций формы аналогичны таковым в теории пластинок. Специфической является потребность описания кривизны конечного элемента, который в общем случае представляется функцией гауссовых координат, позволяющие найти координату любой точки, кривизну в ней по значениям некоторых геометрических параметров в узлах конечного элемента.

Резюме.Конечные элементы оболочек широкого профиля (ориентированные на расчет произвольной оболочки) требует аппроксимации геометрии срединной поверхности по тому же принципу, что и деформированные поверхности. Часто используются конечные элементы, в которых срединная поверхность и деформированная срединная поверхность аппроксимируются одинаковыми функциями формы с одинаковым набором параметров (изопараметрические элементы).

Для оболочек с конкретной формой срединной поверхности более экономично по вычислительным ресурсам оказываются конечные элементы, учитывающие особенности срединной поверхности. В частности, для оболочек вращения часто используют конечный элемент в виде усеченного конуса. Упрощение в этом элементе достигается за счет конкретизации зависимостей кривизны от гауссовых координат

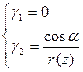
Существуют библиотеки оболочечных конечных элементов, интегрированные в пакеты конечноэлементного анализа.