Некоторые простейшие задачи теории оболочек

Наиболее простой для анализа является оболочка со срединной поверхностью в форме кругового цилиндра. Для нее

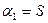
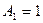
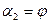
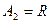
Свойства геометрии цилиндрической оболочки позволяют получить соотношения для деформации оболочки непосредственно, не привлекая общей теории.

Пусть задан поперечный размер оболочки – толщина 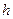. Будем считать, что деформации малы и из элементарных соображений определим деформации материала.

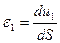
Если нагрузка на цилиндрическую оболочку обладает свойством осевой симметрии, то окружную деформацию 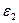можно определить так:

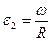
Здесь 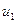- продольное перемещение, 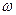- перемещение по нормали к срединной поверхности (прогиб).

Для такой оболочки удается разделить состояние растяжения/сжатия и изгиба.

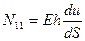
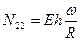
Выписанные соотношения справедливы для случая бесконечно длинной оболочки или оболочки, края которой могут свободно перемещаться в радиальном направлении.

Если такие ограничения присутствуют, то в оболочке возникают изгибающие моменты. Им соответствуют линейные по толщине распределения напряжений, являющиеся следствием гипотезы прямой нормали.

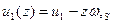
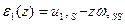
Если подставить эти выражения в уравнение равновесия, из которого предварительно выразив мембранные силы и изгибающие моменты через градиенты перемещений, то получим уравнения изгиба оболочек в виде

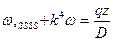
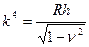
Решение этого уравнения имеет вид:

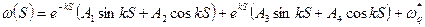
Решение уравнения состояния для цилиндрической оболочки содержит три состояния:

1) быстро затухает при удалении от нуля;

2) быстро возрастает при удалении от нуля;

3) полностью определяется внутренним давлением.

Если предположить, что оболочка полубесконечна, внутреннее давление отсутствует и на краю оболочки 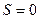сообщается начальное перемещение 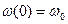, то следует положить 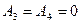(условие ограниченности решения на бесконечности), а из краевых условий в нуле , .

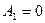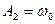Полученное решение затухает по мере удаления от края и на достаточном удалении от него становится пренебрежительно малым.

Это решение выражает особенность состояния оболочки, которое называется краевым эффектом.

Если в той же оболочке добавить равномерно распределенное по длине давление, то соответствующее решение 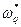будет константой и зависимость решения от координаты 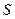примет следующий вид:

За пределами зоны краевого эффекта кривизна оболочки не изменяется, т.е. изгибающие моменты равны нулю. Это означает, что распределение напряжений по толщине оболочки равномерно.

Такое состояние называется безмоментным.

С точки зрения прочности безмоментное состояние является оптимальным, т.к. разрушающее напряжение развивается одновременно по всей толщине оболочки.

Покажем, при каких условиях возможна реализация безмоментного состояния оболочки.

1) ;

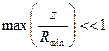2) цилиндрическая жесткость оболочки 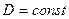(оболочка должна быть однородной по гауссовым координатам);

3) 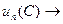свободна, т.е. 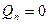. Это условие означает, что краевые условия не должны накладывать ограничения на перемещения края оболочки по нормали.

4) 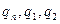- гладкие функции ( 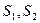); 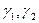- гладкие функции ( ).

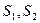Если все четыре условия выполнены, то возможна реализация безмоментного состояния оболочки.

;

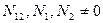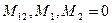
Равенство нулю изгибающих и крутящего моментов позволяет выделить в уравнении равновесия три уравнения проекций мембранных сил на оси подвижного трехгранника:

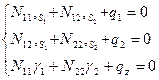
Выделение этих уравнений в самостоятельную группу показывает, что задача о безмоментном состоянии оболочки является статически определимой, мембранные силы могут быть найдены только из уравнений равновесия и краевых условий в усилиях. Если хотя бы одно из четырех условий безмоментного состояния нарушено, то в его окрестности возникает «краевой эффект» состояния изгиба, быстро затухающее по мере удаления от возмущающего фактора.

Задача о безмоментном состоянии оболочки в общем виде также представляет собой существенные математические трудности. Аналитическое решение можно найти для задачи о безмоментном состоянии оболочек вращения, у которых срединная поверхность образована вращением плоской кривой (меридиана) вокруг некоторой прямой, лежащей в плоскости меридианы. Геометрию оболочки вращения полностью определяет уравнение меридианы в координатах .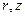

При решении задач равновесия безмоментных оболочек вместо упрощения общих уравнений в теории оболочек воспользуемся свойством статической определимости и для определения усилий 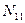и и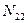спользуем метод сечений.

Для осесимметричной оболочки при осесимметричной нагрузке можно выделить 2 не связанных между собой безмоментых состояния (т.к. )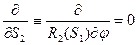

1) Осесимметричное кручение

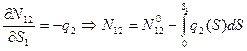
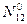определяется из краевого условия, заданного в начале координат крутящего момента, вектор которого направлен вдоль оси .

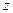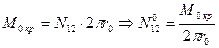
2) Возникает при отсутствии нагрузки 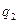и крутящего момента на краю.

В этом случае касательные напряжения на площадках с нормалям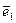и и 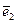отсутствуют и направления 1,2 являются главными.

Поэтому при решении второй задачи можно записать:

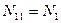
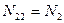
Тогда уравнение равновесия можно переписать в виде:

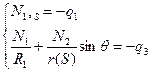
Усилие на краю оболочки 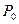определяется из условия равновесия оболочки в целом как абсолютно твердого тела. В качестве уравнения равновесия отсеченной части оболочки используем сумму проекций всех сил на ось вращения.

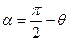
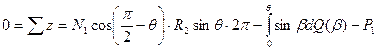
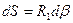
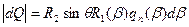
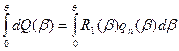
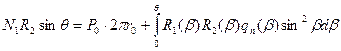
Если оболочка имеет прямолинейную образующую (цилиндр или конус), то вместо угловой координаты 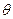следует использовать дуговую координату 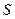или под интегралом исключить из рассмотрения радиус кривизны 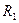, обозначив

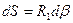
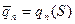
Если рассматривается цилиндрическая безмоментная оболочка открытая с двух концов, находящаяся под действием давления газа, то усилие 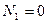, 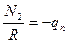. Если рассматривается цилиндрическая оболочка, закрытая с двух концов, то 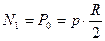, , 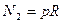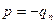. Напряжения в оболочке

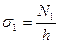
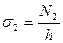
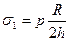
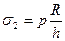
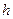- толщина оболочки.

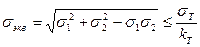- условие прочности для расчета безмоментной оболочки.

Рассмотрим цилиндрическую оболочку под действием внутреннего давления. Будем предполагать, что оболочка имеет конечную длину, и закрепление краев не обеспечивает условий безмоментного состояния. При этом координата 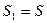отсчитывается вдоль образующей, координата 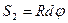, где 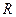- радиус срединной поверхности.

В силу осевой симметрии и равенства нулю первой кривизны ( 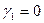), справедливы соотношения

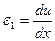
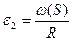
Изменение кривизны меридиана: .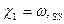

Изменение кривизны параллели: .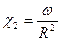

Уравнение равновесия после исключения поперечной силы 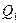имеет вид:

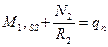
Соотношение обобщенного закона Гука дает:

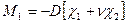
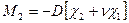
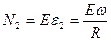
Подставляем полученные выражения в уравнение равновесия и принимаем

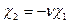
Получаем дифференциальное уравнение состояния в виде:

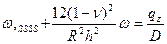
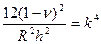
Характеристическое уравнение имеет четыре комплексных корня, что приводит к решению в виде произведения экспоненты на тригонометрические функции

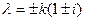
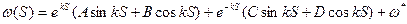
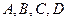определяются из краевых условий.

В этом случае угол поворота нормали отождествляется 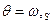. Следовательно, краевые условия становятся такими же как при изгибе стержней. 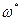- частное решение уравнения состояния для конкретного вида нагрузки .

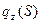При 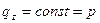: 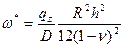, т.е. .

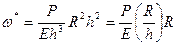В соответствии с видом решения, оболочки классифицируют по длине.

Длинной называют оболочку, для которой 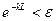, где 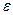- наперед заданная малая величина

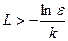
Величина 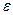- допустимая погрешность от неучета краевого эффекта.

Если .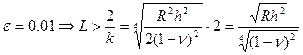

Полученная оценка определяет ширину зоны краевого эффекта. Если длина оболочки больше 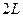, то можно рассматривать края оболочки отдельно, при этом постоянные 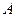и 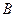в решении равны нулю. В короткой оболочке решение следует сохранить полностью и определять 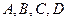из четырех совместно решаемых уравнений.