Элементы теории пластинок
Теория пластинок отличается от общей теории оболочек тем, что криволинейные координаты 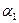 и
и 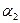 являются декартовыми, базисные векторы
являются декартовыми, базисные векторы 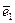 ,
, 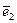 ,
, 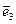 не меняются при движении по срединной плоскости, координатные линии
не меняются при движении по срединной плоскости, координатные линии 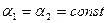 есть прямые. Будем считать, что для пластинки выбор положения осей x, y определен либо формой пластинки в плане, либо направлением главных осей анизотропии материала.
есть прямые. Будем считать, что для пластинки выбор положения осей x, y определен либо формой пластинки в плане, либо направлением главных осей анизотропии материала.
Для ортотропного материала, изготовленного в виде листа, механическими характеристики являются три модуля Юнга, три коэффициента Пуассона, три модуля сдвига, принятые кинематические и статистические гипотезы позволяют исключить из рассмотрения все характеристики материала, связанные с направлением поперек листа: 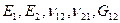 .
.
Требование симметричности упругих постоянных:
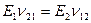
Выражение обобщенного закона Гука:
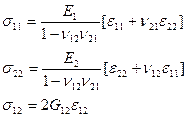 (2.125)
(2.125)
В случае изотропного материала:
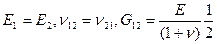 (2.126)
(2.126)
Рассмотрим вариационную формулировку задачи теории пластинки. С этой целью вводим следующие матричные обозначения.
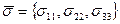 -вектор напряжений,
-вектор напряжений,
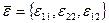 - вектор деформаций.
- вектор деформаций.
Тензор упругих постоянных 4-го ранга представим в виде квадратной матрицы 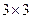 .
.
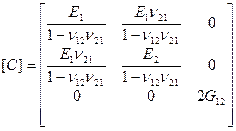
Рассмотрим следствие из кинематической гипотезы Кирхгофа и сформулируем его в матричной форме. В силу специфического выбора системы координат базисные векторы при деформации не изменяются и, производная от поперечного перемещения приобретает физический смысл углов поворота нормали.




Из приведенного рисунка видно, что угол поворота нормали определяется соотношением:
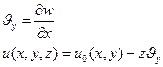 (2.127)
(2.127)
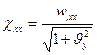 - кривизна линии, получающейся при пересечении координатной плоскости xz и деформированной срединной плоскости.
- кривизна линии, получающейся при пересечении координатной плоскости xz и деформированной срединной плоскости.
Считаем, что 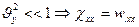 (2.128)
(2.128)
Рассуждая аналогично, получим
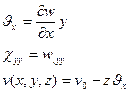 (2.129)
(2.129)
Вычислим компоненты тензора малых деформаций:
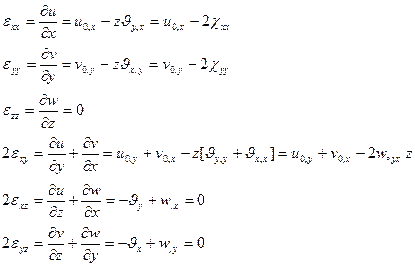 (2.130)
(2.130)
Следствием гипотезы прямой нормали является равенство 0 всех компонент тензора деформации с индексом z и линейное распределение нормальных и касательных напряжений по толщине пластинки. Вычисляя компоненты тензора напряжений в предположении, что оси x,y являются главными осями ортотропии, получим:
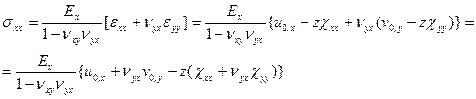
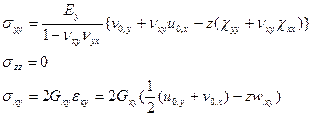 (2.131)
(2.131)
Таким образом, применение статической гипотезы и предположение о справедливости обобщенного закона Гука приводит к линейному распределению нормальных и касательных напряжений по толщине пластинки. Перейдем к матричной форме записи этих соотношений.
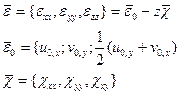 (2.132)
(2.132)
Вектор напряжений: 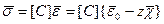 (2.133)
(2.133)
Подставим (2.132), (2.133) в вариационное уравнение Лагранжа.
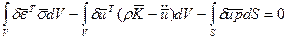
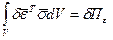 - элементарная работа внутренних сил.
- элементарная работа внутренних сил.
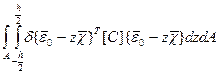
А – площадь, ограниченная контуром срединной плоскости в начальном состоянии (площадь пластинки в плане).
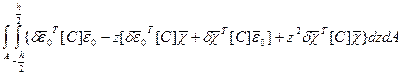
Для пластинок, однородных по толщине деформации  , кривизны
, кривизны 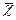 и матрица
и матрица 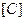 не зависят от z. Тогда интегрирование по z можно выполнить, заметив, что
не зависят от z. Тогда интегрирование по z можно выполнить, заметив, что
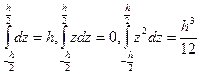
Введем обозначения:

Матрица 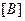 , составленная из произведений постоянных упругости на толщину пластинки, называется матрицей мембранных жесткостей. Матрица
, составленная из произведений постоянных упругости на толщину пластинки, называется матрицей мембранных жесткостей. Матрица 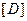 называется матрицей цилиндрических жесткостей. Используя обозначения (2.134), получим:
называется матрицей цилиндрических жесткостей. Используя обозначения (2.134), получим:
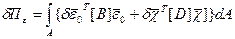 (2.135)
(2.135)
В последнем выражении первое слагаемое зависит только от двух функций 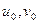 , а второе слагаемое только то w. Рассмотрим слагаемое, описывающее работу массовых сил, включая туда силы инерции.
, а второе слагаемое только то w. Рассмотрим слагаемое, описывающее работу массовых сил, включая туда силы инерции.

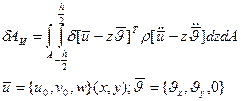
Примем, что пластинка однородная по толщине, 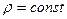 .
.
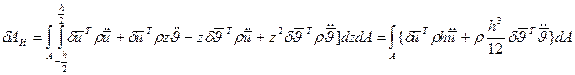 (**)
(**)
Формула (**) учитывает инерцию поступательного перемещения (1-е слагаемое) и инерцию поворота нормального волокна (2-е слагаемое). Для оценки сравнительной величины этих 2-х слагаемых перейдем к безразмерным перемещениям.
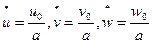
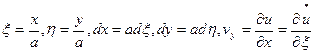
где а – характерный размер пластинки в плане.
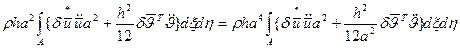
Последняя формула показывает, что если ускорение поступательного движения и поворота нормального волокна имеют один порядок, то соотношение между ними определяются квадратом отношения толщины пластинки к ее характерному размеру в плане, т.е.
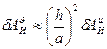
Для тонких пластинок при невысоких частотах колебаний ( 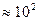 кГц) эта поправка имеет верхнюю оценку 0,01%. В дальнейшем инерцией поворота будем пренебрегать.
кГц) эта поправка имеет верхнюю оценку 0,01%. В дальнейшем инерцией поворота будем пренебрегать.
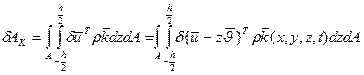
Для тонкой пластинки изменение массовой силы по толщине можно пренебречь, если считать плотность постоянной по толщине, то интеграл по толщине от второго слагаемого равен 0, т.е.
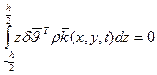
Тогда работу массовых сил запишем в виде:
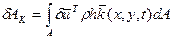 (2.136)
(2.136)
Рассмотрим работу поверхностных сил:
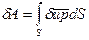
В этой формуле под S понимают всю поверхность пластинки, которая состоит из 3-х частей: две плоскости, отстоящие друг от друга на толщину h (верхняя и нижняя грани пластинки) - 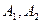 и торцевую поверхность пластинки, которая определяется контуром пластинки в плане и ее толщиной. Интеграл по поверхности пластинки можно разделить на 3 части.
и торцевую поверхность пластинки, которая определяется контуром пластинки в плане и ее толщиной. Интеграл по поверхности пластинки можно разделить на 3 части.
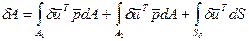
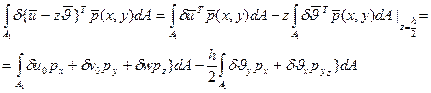
Последнее слагаемое – моменты составляющей нагрузки, параллельной срединной плоскости относительно осей xy имеет порядок 
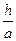 по сравнению с первым слагаемым. Поэтому для тонких пластинок это слагаемое можно опустить. Проводя аналогичные рассуждения для поверхности
по сравнению с первым слагаемым. Поэтому для тонких пластинок это слагаемое можно опустить. Проводя аналогичные рассуждения для поверхности 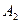 , можно записать работу сил, распределенных по верхней и нижней поверхностям в виде:
, можно записать работу сил, распределенных по верхней и нижней поверхностям в виде:
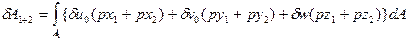 (2.137)
(2.137)
Тем самым мы постулируем, что вместо конкретных распределенных поверхностных сил по верхней и нижней поверхностям пластинки можно использовать эквивалентную нагрузку, распределенную по срединной плоскости. Обращаясь к формулам (2.136), не трудно заметить, что работу массовых сил и работу поверхностных сил 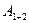 можно объединить. Рассмотрим нагрузку, распределенную по срединной плоскости, компоненты которой определяются как суммы соответствующих компонент массовой нагрузки и нагрузок
можно объединить. Рассмотрим нагрузку, распределенную по срединной плоскости, компоненты которой определяются как суммы соответствующих компонент массовой нагрузки и нагрузок 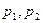 .
.
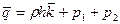
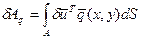 (2.138)
(2.138)
Рассмотрим работу сил, приложенных к боковой поверхности:
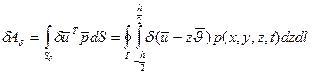
Представим себе, что внешняя нагрузка может быть представлена в виде суммы двух составляющих: одна из них описывается четной функцией z, а другая – нечетной, т.е.
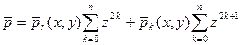
При вычислении интеграла по z, получим:
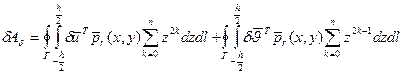
Первое слагаемое можно интерпретировать как нагрузку, распределенную по контуру срединной плоскости, а вторую часть как момент, распределенный по тому же контуру. Для дальнейших рассуждений удобно представить их проекциями на касательную к контуру точки и на нормаль.




Такое распределение удобно тем, что позволяет выделить составляющие контурной нагрузки, для которой обобщенные перемещения являются перемещениями в плоскости пластинки ( 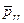 ) и такие, для которых обобщенные перемещения являются поперечное перемещение w и его градиенты
) и такие, для которых обобщенные перемещения являются поперечное перемещение w и его градиенты 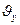 и
и 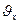 (
( 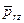 и
и 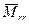 ). Крутящий момент
). Крутящий момент 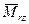 изменяет крутку пластинки
изменяет крутку пластинки 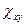 , которая является для него обобщенным перемещением. В практических задачах этот момент обычно равен 0. С учетом сделанных предположений работу сил, распределенных по боковой поверхности можно записать в виде:
, которая является для него обобщенным перемещением. В практических задачах этот момент обычно равен 0. С учетом сделанных предположений работу сил, распределенных по боковой поверхности можно записать в виде:
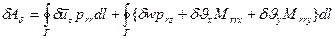 (2.139)
(2.139)
Рассматривая формулу для элементарных работ внешних и внутренних сил не трудно заметить, что в каждой их них можно выделить составляющие, для которых обобщенные перемещения являются компонентами  и
и 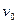 перемещения точки к срединной плоскости и компоненты, для которых обобщенным перемещением являются поперечное перемещение w и его градиенты
перемещения точки к срединной плоскости и компоненты, для которых обобщенным перемещением являются поперечное перемещение w и его градиенты 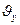 и
и 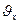 .Т.к.
.Т.к.  и
и 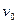 , w есть независимые компоненты перемещения, то можно потребовать отдельного равенства 0 элементарных работ сил на перемещениях
, w есть независимые компоненты перемещения, то можно потребовать отдельного равенства 0 элементарных работ сил на перемещениях 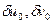 и
и 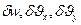 .
.
Тем самым задача о деформации пластинки разделяется на две независимые подзадачи:
1) задача о плоском напряженном состоянии пластинки под действием внешней нагрузки 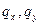 и контурной нагрузки
и контурной нагрузки  .
.
2) Задача об изгибе пластинки под действием поперечной нагрузки 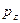 , контурной силы
, контурной силы 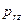 и контурного момента
и контурного момента 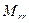 .
.
Аналогичные заключения справедливы и в том случае, если пластинка многослойная, но ее структура обладает свойством симметрии относительно срединной поверхности.
Если же такие свойства отсутствуют, то чаще всего решают связанную задачу, выбирая за плоскость приведения либо верхнюю, либо нижнюю плоскость. Выражение для принципа Лагранже в общих подзадачах имеет вид:
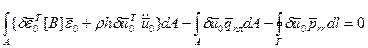 (2.140)
(2.140)
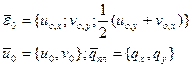
Для изгиба
 (2.141)
(2.141)
Дата добавления: 2015-02-16; просмотров: 972;
