Численное решение задач динамики и статики пластинок

В предыдущих примерах были представлены аналитические решения некоторых задач теории пластинок. Найти их решение в аналитической форме оказалось возможным, т.к. краевые условия были заданы на координатных линиях и удалось подобрать такие формы, решения которых тождественно удовлетворили указанным условиям. При решении реальных задач такое удается крайне редко и поэтому даже для пластинок простой формы определение аналитических решений оказывается невозможным.

Т.к. наиболее общим численным методом решения задач механики сплошной среды является метод конечных элементов, то рассмотрим особенности его применения в теории пластинок. Здесь ограничимся задачами изгиба, т.к. особенности решения задач плоского напряженного состояния рассматривались ранее. Отличием задачи изгиба от плоского напряженного состояния является необходимость гладкой аппроксимации деформированной серединной плоскости.

Пусть имеем

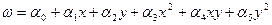
æ

æ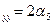

æ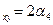

Т.к. обобщенные деформации (кривизна и крутка) срединной плоскости определяются 2-ми градиентами поперечного перемещения 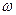, то аппроксимирующие полиномы должны быть не ниже второй степени, что обеспечивает неравную нулю потенциальную энергию деформации. Применение полинома второй степени по двум независимым переменным позволяет построить конечный элемент в виде треугольника с шестью узлами, причем три дополнительных узла следует располагать на серединах сторон. Степенями свободы такого конечного элемента являются поперечные перемещения его узлов. Недостатком этого конечного элемента является постоянство кривизны и крутки в его пределах. Деформированная срединная плоскость оказывается негладкой, угол поворота нормали при переходе через границу соседних конечных элементов может меняться скачком. Упомянутое свойство такого конечного элемента заставляет существенно измельчать сетку. Достоинством является гарантированная сходимость к точному решению при стремлении количества узлов к бесконечности.

Функцию формы такого элемента удобно выразить через барицентрические координаты, представляющие собой относительные площади треугольников, на которые можно разбить площадь конечного элемента, соединяя его вершины с произвольно выбранной внутри конечного элемента точкой.

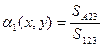
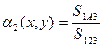
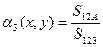
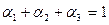
Введенные координаты называются барицентрическими.

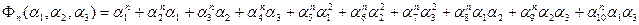
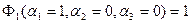
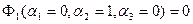
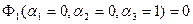
Для узла 1: .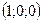

Для узла 2: .

Для узла 3: .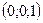

Для узла 4: .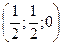

Для узла 5: .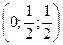

Для узла 6: .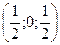

Т.к. полный полином по зреем независимым переменным имеет 10 коэффициентов, а условий всего шесть, то исключим из представления функции формы линейную часть.

Если 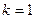, то

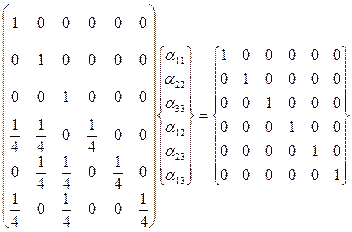
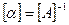
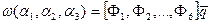
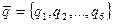
Возможно использование прямоугольного конечного элемента, который обеспечивает непрерывность не только перемещений, но и углов поворота. В этом случае степенями свободы узла следует выбрать поперечные перемещения и два угла поворота.

В качестве функций формы следует выбрать произведение полиномов Эрмита, которые использовались при аппроксимации прогиба в стержнях и обеспечивали непрерывность и гладкость этой аппроксимации.

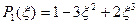
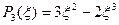
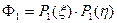- описывает прогиб в узле 1.

,

;

;

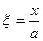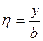
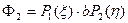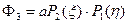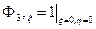
Для остальных узлов комбинации полиномов Эрмита строятся аналогично.

Введем новое обозначение. У функции формы будем указывать индекс, состоящий из двух элементов:

1) номер узла;

2) буквенное обозначение для степени свободы.

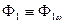
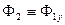
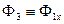
Тогда

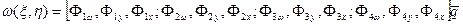
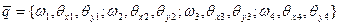
Чтобы избавиться от недостатка, присущего данному элементу (ортогональности сторон), исходную сетку конечных элементов, состоящую из произвольных четырехугольников, следует преобразовать к прямоугольной форме. Такое преобразование может быть построено аналитически или численно. Более удобно для каждого конечного элемента проделать локальное преобразование в единичный квадрат.

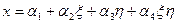
Определение коэффициентов преобразования осуществляется путем решения системы уравнений:

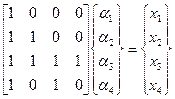
Имея такое преобразование нетрудно построить формулы перехода при интегрировании и дифференцировании от , 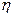к 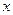, и наоборот.

После выбора функций формы построение матричных характеристик конечных элементов проводится по известному алгоритму, в котором матрица дифференциальных операторов принимает вид:

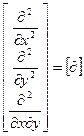
Матрица градиентов функции формы определяется

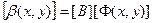
Отличными от нуля будут три компонента тензора деформации и три компонента тензора напряжений. Для вычисления напряжений используется формула

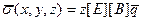
Наибольшее и наименьшее напряжение получается, если

Выражение для компонент матрицы градиента и матрицы функции формы достаточно сложны. При использовании треугольного конечного элемента, произведение градиентов есть 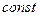, а произведение функций формы имеют четвертую степень относительно координат. При четырехугольном конечном элементе произведение градиентов имеет вторую степень, а функции формы – шестую степень относительно координат.

Для вычисления матриц жесткости и масс, а также вектора нагрузок можно рекомендовать алгоритм, основанный на квадратурной форме Гаусса с количеством узловых точек, зависящим от степени координат. Для треугольного конечного элемента при вычислении матрицы жесткости достаточно одного узла (центра масс конечного элемента) при вычислении матрицы масс и вектора нагрузок – трех узлов. Для четырехугольного конечного элемента количество узлов составляет 3 и 5.