Пример применения метода начальных параметров

Задача: Найти перемещения конца стержня, построить эпюры продольных сил и перемещений.

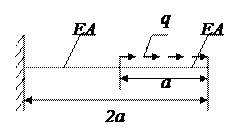
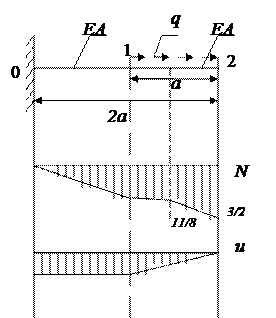
1.разделить стержень на участки. Границами участков служат точки, в которых нарушается регулярность, геометрия стержня, в точности точки приложения сосредоточенных сил. В данной задаче естественными границами являются точки 0, 2 (начало и конец стержня). Точка нерегулярности – точка 1 (распределенная нагрузка возрастает скачком от 0 до q). Условимся нумеровать участки по правому крайнему углу.

2.составление матричных характеристик участков. Для составления основного уравнения потребуется матрица влияния 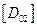и вектор нагрузки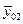

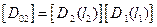
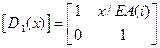i=1,2

,

,

.

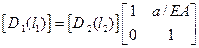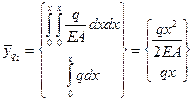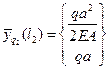
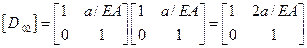3.составление основного уравнения и удовлетворение краевым условиям.

,

.

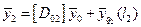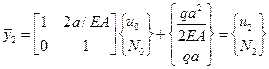Из рисунка видно, что перемещение узла (0) равно нулю ( 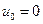), внутренняя сила в узле (2) равна нулю ( 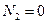). В последнем уравнении вместо 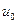подставим 0.

.

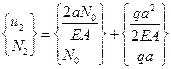Исходя из заданного условия на правом краю ( 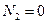) выберем второе уравнение, в котором только одно неизвестное.

4.Определение неизвестных начальных параметров.

,

.

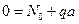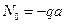5.Построение эпюр. Вектор начальных параметров имеет вид:

.

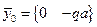Чтобы найти значение вектора состояния на первом участке, используется (2.15) при n=1.

1-ый участок:

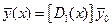
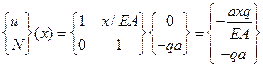
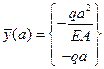
2-ой участок: используем полученное выражение для вектора состояния.

,

,

.

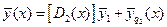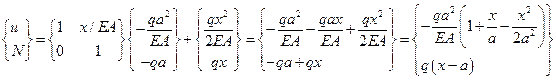
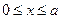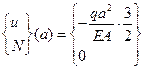
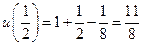Знак “-” в решении получился от того, что значение на начальной внутренний силы 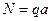определено правильно, а знак “-” показывает направление вектора опорной реакции по отношению к системе координат. В теории стержней принято считать положительной внутреннюю силу, которая направлена от сечения. В этом смысле полученные значения начального параметра 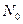при построении эпюр следует считать положительным.

Задача:

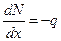
Воспользуемся методом сечений (для статически определимых стержней):

1. Мысленно проводим сечение и отбрасываем ненужную часть. Рисуем оставшийся участок отдельно.

Составим уравнение равновесия: , .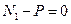

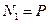2. Отделяем второй участок сечением 2. Также составляем уравнение равновесия для этого участка:

, .

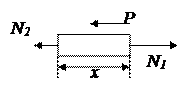
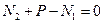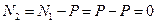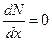, следовательно , .

.

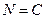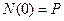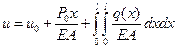Так как отсутствует продольная распределенная нагрузка 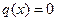, то

.

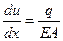Метод сечений отличается тем, что он удобен для решения статически определимых задач, когда не требуется определения перемещений. Метод начальных параметров требует больших вычислительных затрат, но является более общим.

Проверочный расчет: .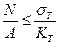

Проектировочный расчет: .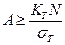

2. Рассмотрим стержень, работающий только на кручение.

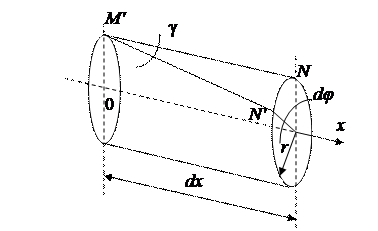Состояние кручения характерно тем, что два близкорасположенных поперечных сечения поворачиваются друг относительно друга на угол φ, причем поворот осуществляется вокруг оси стержня. Угол поворота φ считается бесконечно малым.

Рассмотрим дугу NN'. Длина дуги: .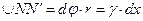

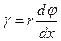. (2.17)

Формула (2.17) выражается соотношением между углом закручивания φ и деформацией сдвига γ. Так как при принятых предположениях удлинение волокон отсутствует, то можно считать, что справедлив закон Гука в следующей формулировке:

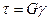(2.18)

где 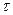- касательное напряжение в плоскости поперечного сечения,

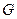- модуль сдвига или модуль упругости второго рода.

.

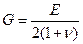Подставляя (2.17.) в (2.18.), получим:

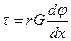(2.19)

Введем понятие внутреннего силового фактора «крутящий момент», который представляет собой главный момент касательных напряжений, действующих в поперечном сечении:

,

.

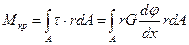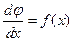Если модель сдвига не зависит от координат поперечного сечения, то соотношение между крутящим моментом и углом закручивания приводится к виду:

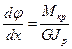(2.20)

где 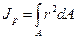- полярный момент инерции поперечного сечения (2.21)

Формула (2.20) – первое уравнение состояния при кручении, связывающее крутящий момент и модуль сдвига.

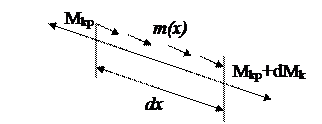
Уравнение равновесия:

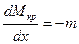(2.22)

Соотношения для закрученного прямого стержня полностью аналогично соотношению для растянутого стержня; отличие заключается только в физическом смысле входящих в уравнение величин. Вместо продольной силы – крутящий момент, вместо продольного перемещения – угол закручивания φ. Вместо жесткости на растяжение ЕА используется жесткость при кручении GJ_p.

В соответствии с этим и методы решения задач о кручении прямых стержней такие же, как при растяжении/сжатии.

3. Рассмотрим стержень, работающий в условиях плоского поперечного изгиба.

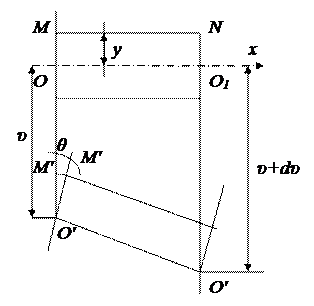
Продольное перемещение: .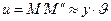

Данное предположение справедливо при малых углах поворотов сечения .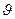

.

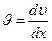Продольное перемещение некоторой точки определяется следующей формулой:

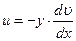(2.23)

Рассмотрим распределение деформации по высоте поперечного сечения:

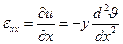(2.24)

.

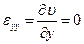Независимость перемещения υ от координаты y является следствием гипотезы плоских сечений Бернулли и предположением о малости угла поворота поперечных сечений.

,

,

,

.

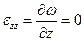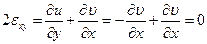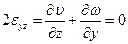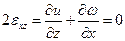Так как в соответствии с (2.24) волокно параллельное оси стержня испытывает только деформации растяжения/сжатия, то отличным от нуля будет только нормальное напряжение в поперечном сечении 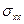и для его вычисления можно использовать закон Гука для одноосного растяжения. Чтобы исключить из рассмотрения напряжения, которые должны возникнуть на площадках с нормалью перпендикулярной оси стержня принимается статическая гипотеза: нормальные напряжения на площадках параллельных оси стержня пренебрежимо малы по сравнению с нормальными в поперечных сечениях.

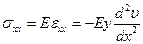(2.25)

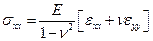, пренебрегаем

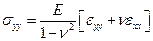, пренебрегаем.

Введем внутренний силовой фактор – изгибающий момент, как главный момент нормальных напряжений, действующих в поперечном сечении относительно оси z.

,

,

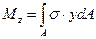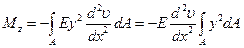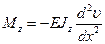(2.26)

где 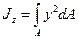- осевой момент инерции поперечного сечения.

Произведение 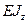- называется изгибная жесткость стержня.

Чтобы замкнуть систему дифференциальных уравнений состояния стержня при изгибе, рассмотрим равновесия участка стержня в указанных условиях. Поперечная сила 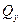- главный вектор касательных напряжений, действующий в поперечном сечении.

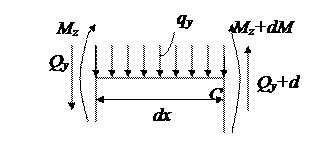
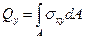(2.27)

в соответствии с (2.24) эта сила должна быть равна нулю, так как сдвиг 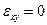. Тем не менее учитывать эти силы надо, так как в противном случае невозможно удовлетворить одному из уравнений равновесия, а именно уравнениям проекции всех сил на вертикальную ось. В этом заключается внутренняя противоречивость кинематической гипотезы Бернулли.

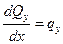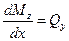, (2.28)

формулы (2.26)-(2.28) описывают состояние стержня.

Есть один случай, для которого гипотеза Бернулли не дает погрешности. Для этого следует потребовать, чтобы 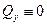. Такое возможно, если стержень изогнуть двумя моментами, приложенными по его концам (чистый изгиб).

Решение задач при изгибе можно реализовывать двумя способами. Если стержень статически определим, то есть опорные реакции можно найти из уравнения равновесия стержня как абсолютно твердого тела, то удобно использовать метод сечений, то есть сначала решить систему уравнений (2.28) и найти распределение по длине изгибающего момента 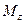. А затем интегрируя (2.26) найти распределение перемещений и угол поворота. Если стержень статически неопределим, то следует использовать метод начальных параметров.