Жидкости. Формула Дюпюи

При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины, поэтому давление и скорость фильтрации зависят только от одной коор­динаты r. При этом во всех горизонтальных плоскостях поле скоростей и давлений будет одинаковым.

Частным случаем плоскорадиального фильтрационного потока яв­ляется приток к гидродинамически совершенной скважине, вскрывшей горизонтальный пласт бесконечной протяженности, мощностью h и сообщающейся с пластом через пол­ностью открытую боковую поверхность цилиндра, отделяющую ствол скважины от продуктивного пласта.

Поток будет также плоскорадиальным при притоке к совершенной скважине радиуса 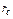(или оттоке от скважины), расположенной в центре ограниченного горизонтального ци­линдрического пласта мощностью h и радиусом R_K (рис. 4.5). Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление 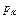, а на забое скважины постоянное давление 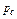, пласт однороден по пори­стости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:

(4.27)

где 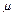- динамический коэффициент вязкости.

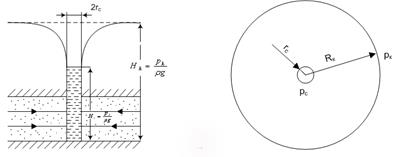
Рис. 4.5. Расчетная схема при плоско-радиальном движении

Закон распределения давления определяется по одной из формул:

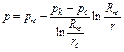, (4.28)

(4.29)

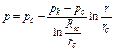(4.30)

Линия 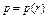называется депрессионной кривой давления. Характерно, что при приближении к скважине градиенты давления и скорости фильтрации резко возрастают. При построении карты изобар следует учитывать, что радиусы изобар изменяются геометрической прогрессии, в то время, как давление на изобарах изменяется в арифметической прогрессии.

Индикаторная линия - зависимость дебита скважины от депрессии 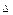р=р_{к -}р_с, при притоке к скважине в условиях справедливости закона Дарси представляет собой прямую линию, определяемую уравнением Q = K 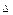p.

Коэффициент продуктивности

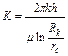(4.31)

численно равен дебиту при депрессии, равной единице.

Закон движения частиц вдоль линии тока, если при t = 0 частица находилась в точке с координатой 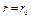, описывается уравнением.

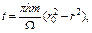(4.32)

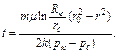(4.32а)

Средневзвешенное по объему порового пространства Ω пластовое давление

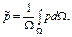(4.33)

где

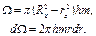
Подставляя выражение для р (4.28), выполняя интегрирование пренебрегая всеми членами, содержащими 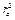, получим

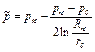(4.34)

Несложно заметить, что индикаторная линия при нарушеннии закона Дарси является параболой.

Если фильтрация происходит по закону Краснопольского, то дебит определяется по формуле

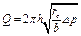(4.35)