Далее по формулам (6.17) и (6.20) находим
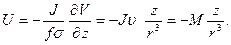(7.1)
Начало координат совмещено с центром шара (рис.7.2).
Учитывая, что r2=x2+z2, M=J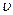 
, z=h, получим
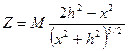, (7.2)
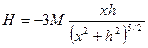. (7.3)
На рис. 7.3 приводим графики Z, Н и Т для вертикально намагниченного шара. В случае его косого намагничивания обратимся к формуле
,
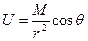где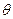 
– угол (Jˆr). Продолжив 
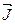до пересечения с координатной плоскостью ХZУ, получим точку Р (х,у,z) и ее азимут А. Вводя углы Ψ и Ψ0 (рис.7.4), по основной формуле сферической тригонометрии можем написать
cos Ψ cos Ψ0+sin Ψ sin Ψ0 cos A.
Выразив тригонометрические функции через прямоугольные координаты, получим
.
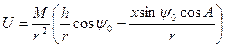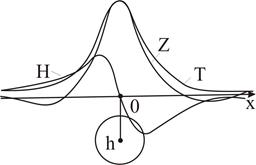
Рис. 7.3. Магнитное поле вертикально намагниченного шара
Если провести ось х через точку Ро, то А=0,и поэтому
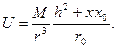
0 Р
А х
Po
Ψ
у 
Ψ0
М
z
Рис. 7.4. К выводу формул Za и На для косо намагниченного шара
Дата добавления: 2015-02-16; просмотров: 1115;