Тогда формулы для косо намагниченного шара приобретут вид
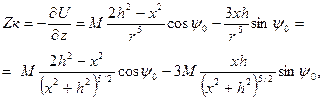 (7.4)
(7.4)
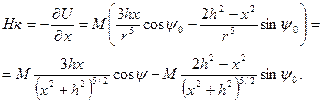 (7.5)
(7.5)
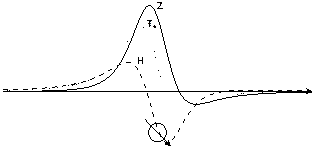
Рис. 7.5. Кривые Z, Н и Т над косонамагниченным шаром
Если учесть, что Ψ= 90 – J, то при сопоставлении с формулой (6.21) обнаруживаем, что ΔТ и Zкос выражаются одинаковыми формулами. Формулы (7.4) и (7.5) можно представить в виде
Zк = Zв cos Ψ0 - Hв sin Ψ0,
Нк = Zв sin Ψ0 + Hв cos Ψ0.
Приводим графики функций Z, Н и Т (рис.7.5) над косонамагниченным шаром.
На основании разложения графиков Zк и Нк можно получить графики Zв и Нв. Для этого необходимо знать эпицентр шара. Если относительно эпицентра найти полусуммы и получить разности, то можно убедиться, что полусумма равна Z в и полуразность ‑ Н в.
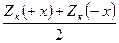 и
и 
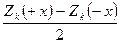 , (7.6)
, (7.6)
Рассмотренный способ разложения графиков аномалий при косой намагниченности на графики при вертикальной намагниченности применим для тел, симметричных относительно плоскости, перпендикулярной оси х, когда графики Zв симметричные, а Нв. ‑ антисимметричные.
Основная трудность заключается в определении положения эпицентра. Если по геологическим данным достоверность определения вызывает сомнение, то задачу можно решить путем подбора. Графики полусумм и полуразностей в наилучшей степени удовлетворяют требуемым условиям, они могут быть использованы для определения эпицентра геологического объекта.
Дата добавления: 2015-02-16; просмотров: 908;
