Простирания

Горизонтальный круговой цилиндр можно заменить дипольной линией: она эквивалентна объемному распределению намагниченного вещества цилиндра. Круговой цилиндр является простейшим двухмерным телом.

На рис.7.6,а дан разрез поперечного сечения горизонтального кругового цилиндра. По формуле Пуассона находим

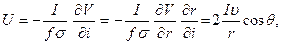(7.7)

где V ‑ гравитационный логарифмический потенциал, определяемый по формуле

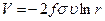. (7.8)

0 x P x

r θ

J

а

z

в

Рис.7.6. Магнитное поле Za для косонамагниченного цилиндра:

а – разрез поперечного сечения горизонтального кругового цилиндра, в – магнитное поле цилиндра

Согласно рисунку (7.6,а) θ = Ψ₀ - Ψ, поэтому, развертывая cos (Ψ₀-Ψ), получим

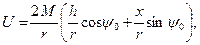
где М ‑ магнитный момент поперечного сечения.

Далее находим составляющие магнитного потенциала:

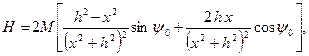(7.9)

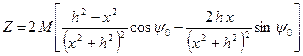. (7.10)

Аномальные кривые Z, Н и Т представлены на рис. 7.6,в.

Если Ψ₀ =0, тосоставляющие Z и Н при вертикальной намагниченности вычисляются по формулам

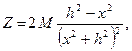
(7.11)

.

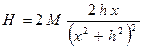
Рис. 7. 7. Магнитное поле горизонтального цилиндра

Вид аномальных кривых для горизонтального цилиндра намагниченного вертикально показан на рис. 7.7.

Очевидно, как и в случае шара,

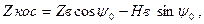
(7.12)

.

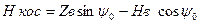Свойства и особенности аномальных графиков Z_кос и Н_кос по профилю для двухмерного цилиндра и шара идентичные.