Вертикальный двухмерный пласт шириной 2в
Рассматривая эффект (рис. 7.10,a) в качестве элементарного тонкого пласта и полагая m=J dξ, имеем
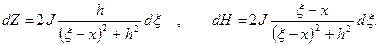
 |



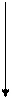
 0 х Р х
0 х Р х


 r1 r2 θ1
r1 r2 θ1

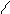




 А В θ2
А В θ2
 |
z
а
в 
Рис. 7.10. Магнитное поле пласта большой мощности
а – модель пласта, в – магнитное поле пласта
Выполняя интегрирование в пределах от –b до b, получим (рис. 7.10,в)
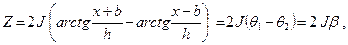 (7.16)
(7.16)
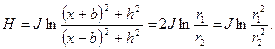 (7.17)
(7.17)
7.3.4. Наклонный пласт большой мощности
Если сдвинуть пласт по направлению вектора J (рис. 7.10), то эффект от объемного распределения можем представить суммой эффектов от трех пластов: АВ, АС и ВD. При этом точки С и D находятся на бесконечности. Если α ‑ угол наклона пласта, то проекции Z, перпендикулярные линиям АС и ВD, будут равны J cos α и –J cos α.
Эффект от пласта АВ получаем по формулам (7.16, 7.17). Для вычисления эффектов от пластов АС и ВD целесообразно ввести вспомогательную систему координат, вертикальная ось которой (z) перпендикулярна соответствующим пластам (рис.7.11).
Для величин во вспомогательной системе координат, отмеченных штрихами, будем иметь
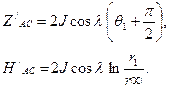
Дата добавления: 2015-02-16; просмотров: 802;
