Анализ процессов фильтрации в пластах различной геометрии
Задача:1. Для каждого пласта различной геометрии рассчитать время (в часах) при котором:
1) процесс фильтрации можно рассматривать как при работе бесконечного пласта;
2) наступает процесс псевдоустановившейся фильтрации;
3) возможно применение уравнения для псевдоустановившегося потока при расчете с точностью 1%.
2. Рассмотреть пластовые системы:
1) со скважиной в центре цилиндрического пласта;
2) со скважиной в центре квадратного пласта;
3) со скважиной в центре одного из квадрантов квадратного пласта.
Для каждого случая: А = 1,7 106 м2, m = 0,2, μ = 1сП, β = 10-4 1/ат,
k = 100 мД.
3. Для каждой скважины по п.1 оценить продуктивность и дебит при
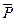 -Pс = 35 ат, если h = 3 м, rc = 0,1 м,
-Pс = 35 ат, если h = 3 м, rc = 0,1 м,
В = 1,2 м3/ м3, S = 4.
4. Для скважин в центре одного из квадрантов квадрата записать уравнения связи дебита и перепада давления при времени 30, 200, 400 часов.
Решение:
1. Прежде всего, рассчитаем комплексный параметр
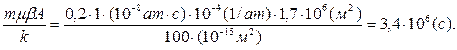
Далее составим следующую таблицу (значения берем из таблицы 1.3.2).
| Геометрия пласта | Решение для бесконечного пласта | Псевдоустановив-шийся поток (приближенное реш.) | Псевдоустановив-шийся поток (точное решение) | |||
| t DА | t (час) | t DА | t (час) | t DА | t (час) | |
| Цилиндрический; cкв в центре | 0,10 | 94,4 | 0,06 | 56,6 | 0,10 | 94,4 |
| Квадрат; cкв в центре | 0,09 | 85,0 | 0,05 | 47,2 | 0,10 | 94,4 |
| cкв. в центре квадранта | 0,025 | 23,6 | 0,30 | 38,3 | 0,60 | 566,4 |
Для цилиндрического пласта со скважиной в центре цилиндра совпадение значений времени для применения решений для бесконечного пласта и для псевдоустановившегося потоков не является ошибочным.
2. Расчет продуктивности и дебита производим на основе уравнений
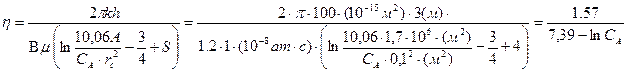 и
и
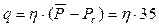 .
.
Таким образом, можно получить следующую нижеследующую таблицу.
| Геометрия пласта | СА | 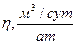
| 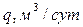
|
| Цилиндрич., скважина в центре | 31,62 | 5,24 | |
| Квадрат, скважина в центре | 30,88 | 5,24 | |
| Скважина в центре квадранта | 4,513 | 2,33 |
3. а) При t = 30 час пласт можно рассматривать как бесконечный и расчетная формула будет иметь вид:
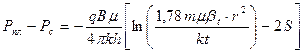 .
.
б) для t = 200 час пласт уже нельзя рассматривать как бесконечный, уже достигнуто псевдоустановившееся состояние и тогда возможно пользоваться уравнением для цилиндрического пласта (1) и квадратного (2).
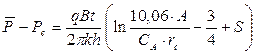 .
.
Однако для скважины в центре одного из квадрантов при t = 200 час точной формулы для расчета характеристик поток пока нет, и следует пользоваться приближенной.
в) Все то же, что и в б) характерно для всех рассматриваемых случаев и при t = 400 час.
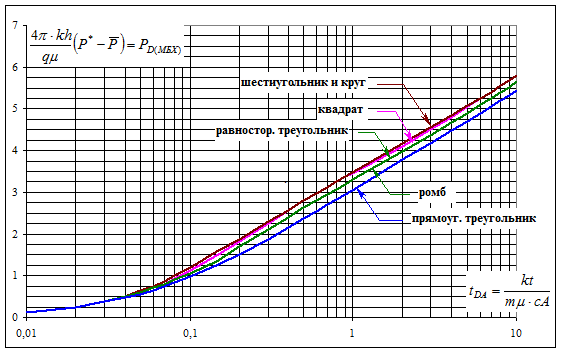
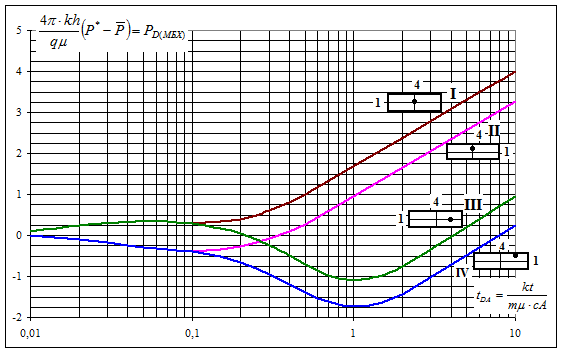
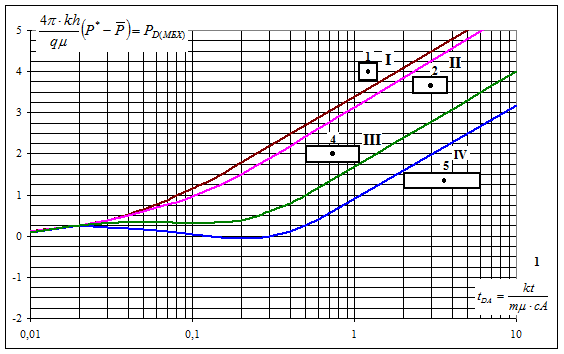
Matthews, Brons и Hazenbroek вычислили и построили графики для функции 4πtpDA+F(tp) = PD MBH для различных конфигураций «скважина-пласт» для различных граничных условий [ ]. Результаты вычисления представили в виде графиков в координатах 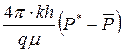 - tDA, где tDA – безразмерное время притока. Полученные графики показаны на рисунках 1.3.7 – 1 3 10 и представляют собой индивидуальные графики для площадей с различной геометрией и для добывающих скважин с различным асимметричным расположением с учетом бесперечточных границ.
- tDA, где tDA – безразмерное время притока. Полученные графики показаны на рисунках 1.3.7 – 1 3 10 и представляют собой индивидуальные графики для площадей с различной геометрией и для добывающих скважин с различным асимметричным расположением с учетом бесперечточных границ.
С помощью этих палеток можно определить среднее давление в пласте.
|
Рис. 1.3.7. Графики МВН для скважины, расположенной в центре площади дренирования правильной формы [ ]
|
б)
|
Рис. 1.3.8. Графики МВН для скважины, расположенной на площади
Дата добавления: 2015-01-15; просмотров: 2013;