Радиальный поток в бесконечном пласте при влиянии емкости скважины
Решение уравнения диффузии для радиального потока включает учет эффекта продолжающегося поступления жидкости после остановки скважины, работавшей до этого длительное время с постоянным дебитом. Этот эффект называют скважинным эффектом и, как показано на рисунке 1.3.11, он связан с накоплением жидкости в трубах.
|
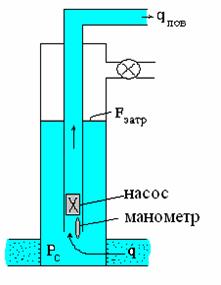
Рис. 1.3.11. Схема поступления пластового флюида в скважину
Исходно в скважину жидкость не поступает, так как столб жидкости в ней компенсирует пластовое давление. Поэтому жидкости в пласте и скважине находятся в равновесии. Если откроем устьевые задвижки и вызовем приток жидкости каким-либо способом, то первые порции жидкости будут поступать на поверхность за счет жидкости из затрубного пространства, где уровень начнет снижаться. Притока жидкости из пласта в самые начальные промежутки времени после пуска скважины в работу не будет, то есть дебит из пласта будет равен нулю. Продолжая отбор жидкости из лифтовых труб на поверхности с постоянным дебитом, дебит поступающей жидкости из пласта будет постепенно приближаться к дебиту устьевому, а снижение уровня жидкости в затрубном пространстве будет приближаться к какому-то постоянному значению.
Установим связь между дебитом на забое (в интервале перфорации) и на поверхности. Предполагаем, что в скважину на забое поступает газожидкостная смесь (рис. 1.3.11) и подача жидкости на поверхность осуществляется каким-либо способом (механизированным или на основе газлифта).
Рассмотрим в общем случае ситуацию, когда на поверхности дебит является переменным.
Материальный баланс масс на забое определится как дебит на забое поступающей в НКТ жидкости qповB, дебит жидкости из пласта qB и дебит (или расход) жидкости, связанный с изменением объема уровня в затрубном пространстве при снижении динамического уровня:
,
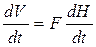где V - объем жидкости в затрубном пространстве, F - площадь сечения скважины в кольцевом пространстве, Н – высота уровня жидкости в затрубном пространстве.
При постоянной площади сечения затрубного пространства F и постоянном объемном факторе В баланс поступающих жидкостей в трубы за счет притока из затрубного пространства и из пласта будет выглядеть следующим образом:
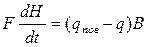, (1.3.22)
где q здесь и ранее - доля дебита жидкости в поверхностных условиях, соответствующая поступившей из пласта жидкости.
Если на поверхности давление равно Ру, то в скважине давление определится как
Рс = Ру + Нγ. (1.3.23)
Тогда
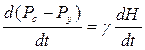. (1.3.24)
Определим емкостную постоянную накопления жидкости в скважине
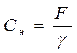, (1.3.25)
где индекс «н» в емкостной постоянной записан для характеристики природы влияния ствола скважины на процессы, происходящие на забое, а именно – связанные с накоплением жидкости в стволе.
Тогда
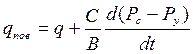. (1.3.26)
При неизменной величине устьевого давления
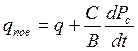. (1.3.27)
Для лучшего понимания решения для рассматриваемого случая влияния эффекта поступления жидкости в скважину после ее остановки, анализ будем проводить при использовании всех переменных и постоянных в исходном уравнении, записанных в безразмерной форме. Допустим qн - начальный дебит на поверхности в момент времени t = 0. Преобразуем уравнения в безразмерную форму записи
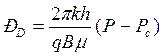, (1.3.28)
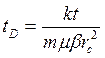. (1.3.29)
Для производной давления в скважине в соответствии с безразмерными характеристиками РD и tD получим зависимость
(1.3.30)
Тогда, согласно (1.3.27) и (1.3.301), получаем
. (1.3.31)
Емкость С запишем также в безразмерной форме
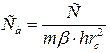. (1.3.32)
Тогда
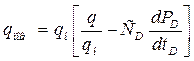. (1.3.33)
Для постоянного дебита, когда q(t) = qн, уравнение (1.3.33) приобретает вид
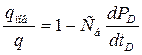. (1.3.34)
Последнее уравнение является ничем иным, как характеристикой условий фильтрации на внутренней границе пласта, то есть граничным условием для слабосжимаемой жидкости при наличии емкостного влияния скважины. Очевидно, для малых СD или для малых значений dPD/dtD - qпов/q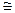 
1, (то есть эффект влияния емкости скважины на изменение забойного давления становится ничтожно малым).
Другой пример связан с условиями скважины, в которую поступает однофазный флюид (жидкость или газ). На поверхность флюид поступает с постоянным дебитом. Рассматривается случай, когда скважинная жидкость объемом V сообщается с пластом и изолирована (например, пакером) и имеет сжимаемость βс (рис. 1.3.12).
Как и ранее, исходя условий материального баланса вытесняемого на поверхность флюида qповВ, и поступающих флюидов из пласта qВ и из затрубного пространства qзатр = VβсdPс/dt, можно записать следующее уравнение
qповВ - qВ = VβсdPс/dt
или
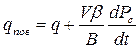. (1.3.35)
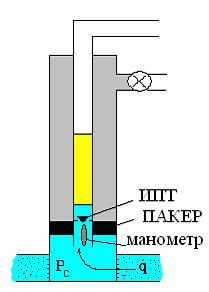
Рис. 1.3.12. Схема поступления пластового флюида в скважину, в которой установлен пакер.
В рассматриваемом случае
Сс=Vβ , (1.3.36)
где индекс «с» в емкостной постоянной записан для характеристики природы влияния ствола скважины на процессы, происходящие на забое, а именно – связанные со сжатием жидкости в стволе скважины.
Поэтому уравнение (1.3.36) принимает вид:
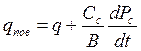. (1.3.37)
Уравнение (1.3.38) идентично уравнению (1.3.27) и отличается только разной записью емкостного параметра С.
В то же время заметим, что сделанное допущение о постоянстве емкостного показателя не годится для газовых скважин, в которых этот показатель не постоянный. Приблизительно СD=1/Рсб .
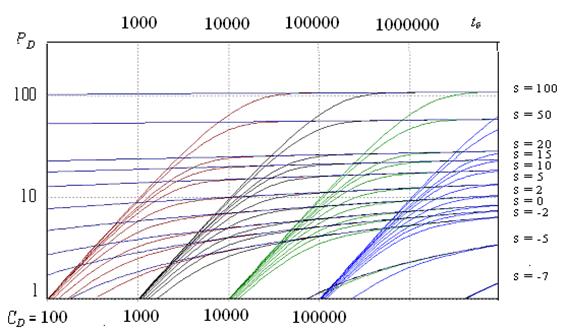
Поскольку уравнения (1.3.37) и (1.3.27) идентичны, то идентичны и уравнения (1.3.33) и (1.3.34) для внутренней границы в бесконечном пласте, при начальном пластовом давлении и загрязненном или стимулированном пласте (характеризуемом соответствующим скин-эффектом S), которые получены аналитическим и численным путем [6, 7]. В ТюмГНГУ выполнены исследования по этой теме и построены аналогичные [6, 7] графики, но для большего диапазона значений функции давления. Эти аналитические решения представлены на рисунке 1.3.13. По графикам на рисунке 1.3.13 значения РD (а также Рс) могут быть вычислены для скважин с известными характеристиками tб , CD и S.
|
Рис. 1.3.13. Эталонные графики снижения давления
Дата добавления: 2015-01-15; просмотров: 2623;