Обзорная информация и экспрессные способы решения прямой задачи

Долгое время решение прямых задач производилось при помощи ручных вычислений. Разработка способов решения прямой задачи для различных тел при разных направлениях вектора намагниченности представляла определенный интерес. В книге В.В. Колюбякина и М.И. Лапиной «Обзор способов решений прямой и обратной задачи магнитной разведки» (М.:Изд-во АН СССР, 1960) проведены фундаментальные исследования по решению прямых задач, рассмотрены решения при различных намагниченностях для трехмерных тел в виде горизонтальных и наклонных отрезков, квадратов, дисков цилиндров, сегментов, полушарий, эллипсоидов, параболоидов и других двухмерных тел. Для группы тел отрезок–полушарие приведены решения 24 задач, для эллипсоидов, эллиптических цилиндров и различных параболоидов – 16 задач. Вычисления выполнены с использованием довольно подробных развернутых таблиц. Приведенные графики имеют иллюстративное значение.

В книге Д.С. Микова «Атлас теоретических кривых для интерпретации магнитных и гравитационных аномалий» (Томск; 1955, позже атлас был переиздан в Москве) приведены графики магнитных аномалий для многих модельных тел, сохраняющих метрологические свойства. Г.Е. Константинов и Л.С. Константинова составили «Альбом теоретических кривых пространственного распределения магнитного поля от моделей».

Кроме аналитических способов решения прямых задач рассмотрены графические с использованием палеток, номограмм и диаграмм. Приведены формулы, таблицы, по которым могут быть построены палетки, а также даны их графические изображения. Диаграммы Z-поля построены в основном для эллиптических тел. Применение их очень упрощает решение задач.

Номограммы ‑ функциональные графики, облегчающие вычисления. Семейства этих графиков приведены для групп различных тел.

Z 0 P x θ1 А В θ2 θ3 θ4 J z С D D

Рис. 7.17. Магнитное поле над мощным пластом, ограниченным снизу

Прямые задачи, их решения и формулы имеют различную сложность и практическую значимость. Рассмотрим экспрессные методы их решения, т.е. такие, при которых оценочные результаты могут быть получены без применения специальной вычислительной техники.

Прежде всего исследуем двухмерное тело вертикального намагничения с сечением в виде прямоугольника. Сдвигая тело по направлению вектора J, получаем две пластинки (рис.7.17) и по формуле (7.16) найдем

Z=2 J (θ₁ - θ₂ - θ₃ - θ₄) . (7.25)

Результат, полученный по этой формуле, только на несколько процентов отличается от величины магнитного эффекта намагниченного вертикального сжатого эллиптического цилиндра. Если В и D отнести на бесконечность, то получим эффект от вертикального контакта мощностью АС. Если точку С отнести на бесконечность, то получим эффект, обусловленный влиянием полуплоскости.

При вычислениях весьма эффективной может быть замена квадрата равновеликим по площади кругом, или наоборот. Чтобы судить о точности замены, рассмотрим следующий пример. Пусть дан квадрат со стороной a на глубине также а. При вычислении Z в эпицентре по формуле (7.1) имеем

.

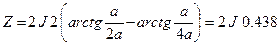В случае круга при вычислении по формуле (7.11) необходимо учесть, что магнитный момент rn=J a² и глубина центра h=1.5 a. Следовательно,

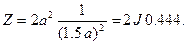
Как видим, разность двух результатов, вычисленных по различным формулам, равна 0.006, что в относительном выражении составляет немногим больше 1%. С удалением расстояния точки вычисления от эпицентра относительная величина разности остается примерно на таком же уровне.