Возведение в степень и извлечение корня из комплексного числа удобно производить тогда, когда комплексное число задано в тригонометрической форме.
Пусть z = r (cos j + i sin j). Найти zn – значит повторить сомножителем z n раз. Тогда на основании известных правил умножения комплексных чисел, будем иметь:
zn = [ r (cos j + i sin j)]n = rn (cos n j + i sin n j);
zn = rn × (cos n j + i sin j) (3)
Формула (3) называется формулой Муавра и показывает, что при возведении комплексного числа в целую положительную степень модуль возводится в эту степень, а аргумент умножается на показатель степени.
Число w называется корнем степени n из числа z,если wn = z.
w = S (cos 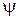 + i sin
+ i sin 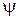 ); z = r (cos j + i sin j);
); z = r (cos j + i sin j);
[S (cos 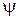 + i sin
+ i sin 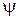 )]n = r (cos j + i sin j)
)]n = r (cos j + i sin j)
Sn (cos n 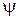 + i sin n
+ i sin n 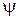 ) = r (cos j + i sin j).
) = r (cos j + i sin j).
Два комплексных числа в тригонометрической форме равны, когда их модули равны, а аргументы отличаются на число, кратное 2p.
r = Sn Þ S = 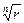 ;
;
n 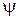 = j + 2kp ;
= j + 2kp ; 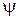 =
= 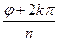 ;
;
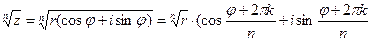 ),
),
где k = 0, 1, 2… (n – 1).
Придавая k n различных значений 0, 1, 2… (n – 1), получим n различных значений корня.
Для контроля усвоения задать вопрос: Выполнить действия:
1. ( 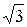 - i)9. Ответ: 512 i
- i)9. Ответ: 512 i
2. 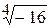 .
.
Ответ: z0 = 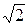 + i
+ i 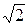 , z1 = -
, z1 = - 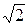 +i
+i 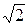 , z2 = -
, z2 = - 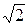 -i
-i 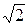 , z3 =
, z3 = 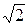 -i
-i 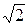 .
.
Вывод: Таким образом, с помощью формулы Муавра можно извлечь корень из комплексного числа и возвести его в любую степень. При извлечении корня из комплексного числа необходимо находить все значения результата. Количество ответов равно степени корня.
Дата добавления: 2015-03-26; просмотров: 1904;
