Действия над комплексными числами в показательной форме
Показательная форма записи комплексных чисел является наиболее удобной для умножения, деления, возведения в степень и извлечения корней из комплексных чисел. Покажем основные соотношения, с помощью которых выполняются эти действия.
Пусть заданы два комплексных числа в показательной форме записи:
Z1 = r 1× e ij1, Z2 = r 2× e ij2.
Произведение этих чисел равно:
Z1 Z2= r 1 r 2× e i(j1+j2).
Частное от деления чисел определяется по формуле:
Z1 /Z2= r 1 /r 2× e i(j1-j2).
Возведение в целую степень n осуществляется по правилу:
(r × e ij)n = (r )n× e inj.
Для извлечения корня целой степени n используется формула:
 , k=0;1;2;…;n-1.
, k=0;1;2;…;n-1.
Для сложения или вычитания комплексных чисел, заданных в показательной форме, необходимо их перевести вначале в алгебраическую форму.
Для закрепления усвоения материала пример:
Вычислить комплексное число, записав его в показательной форме:
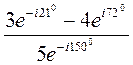 .
.
Решение:
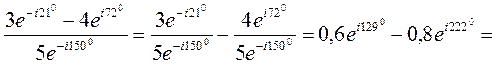
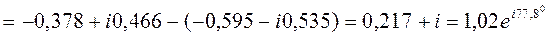 .
.
Вывод:При сложении и вычитании комплексных чисел используется алгебраическая форма записи. При умножении, делении, возведении в степень и извлечении корня наиболее подходящей является показательная форма записи комплексных чисел.
Дата добавления: 2015-03-26; просмотров: 3334;
