Операции над комплексными числами в алгебраической форме
Сложение комплексных чисел
Суммой двух комплексных чисел x1 + iy1 и x2 + iy2 называется комплексное число, определяемое равенством.
(x1 + iy1) + (x2 + iy2) = (x1 + x2) + i (y1 + y2) (1)
Вычитание комплексных чисел
Разностью двух комплексных чисел x1 + iy1 и x2 + iy2 называется такое комплексное число, которое будучи сложено с x2 + iy2, даёт в сумме x1 + iy1.
(x1 + iy1) – (x2 + iy2) = (x1 – x2) + i (y1 – y2) (2)
 |
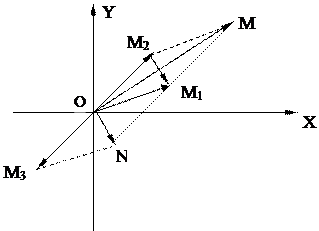Из формул 1 и 2 следует, что сложение и вычитание комплексных чисел, изображённых векторами, производится по правилам сложения и вычитания векторов.
, 
,
, 
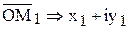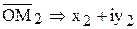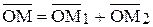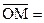(x1 + x2) + i (y1 + y2),
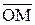3 = - (x2 + iy2) , 
,
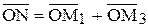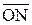= (x1 - x2) + i (y1 - y2), = 
.
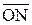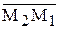Аналогично, можно показать, что комплексные числа можно умножать на вещественные числа так же, как векторы на скаляры.
Дата добавления: 2015-03-26; просмотров: 965;