Деление комплексных чисел. Деление комплексных чисел определяется как действие обратное умножению:

Деление комплексных чисел определяется как действие обратное умножению:

z₁ = х₁ +iу₁; z₂ = х₂ +iу₂; 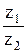= z₃ ; z₃ = x₃ + iy₃.

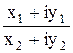= x₃ + iy₃ ; x₁ + iy₁ = (x₂ + iy₂)(x₃ + iy₃);

x₁ + iy₁ = (x₂ x₃ – y₂y₃) + i(x₂y₃ + y₂x₃);

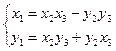
Решая систему уравнений, получим:

x₃ = 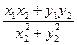; y₃ =

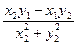
тогда z₃ = 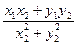+ i .

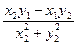Следовательно, умножив делимое и делитель на число, сопряженное делителю, получим в делителе действительное число. Затем разделим на это действительное число действительную и мнимую части делимого, получим частное.

Для контроля усвоения задать вопрос: Выполнить действия над комплексными числами:.

1) (2а – 3bi) + (–a – bi) + (4a + 2bi) – (2a – 5bi). Ответ: 3a + 3bi

2) (5 + 2i)(2 + 3i). Ответ: 4 + 19i

3) 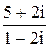. Ответ: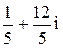

Вывод:Комплексные числа, заданные в алгебраической форме, можно складывать, умножать и делить по правилам алгебры действительных чисел, имея в виду значение квадрата мнимой единицы: i²=-1.

2. Умножение и деление комплексных чисел в тригонометрической форме