Формула Эйлера. Показательная форма комплексного числа.

Во многих случаях использования комплексных чисел применяется показательная форма их записи. Для получения этой формы используется формула Эйлера:

,

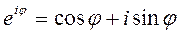вывод которой основывается на знании степенных рядов.

Представим комплексное число в тригонометрической форме:

z = r (cos j + i sin j)

На основании формулы Эйлера получим показательную форму комплексного числа:

z = r × e ^ij.

Для перехода от алгебраической формы записи комплексного числа к показательной воспользуемся известными формулами:

r = 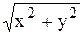, j = arctg .

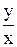Вычисление аргумента по приведенной формуле рекомендуется производить с осторожностью. Следует правильно определять знак аргумента с учетом расположения комплексного числа на комплексной плоскости и следить за тем, чтобы абсолютное значение аргумента не превышало p.

Для контроля усвоения задать вопрос: Записать комплексное число

z = –1 + i в показательной форме.

Ответ: –1+ i =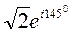

Вывод:Формула Эйлера позволяет представить комплексное число в показательной форме, представляющей произведение модуля комплексного числа на экспоненту. Показатель степени в экспоненте мнимый, его коэффициентом является аргумент комплексного числа.