Алгебраическая форма комплексного числа и изображение его на комплексной плоскости

Определение. Комплексными числами называются выражения вида x+ yi , где x, y – вещественные числа, а i - мнимая единица.

z = x + iy

x – вещественная часть комплексного числа: x = Re z;

iy – мнимая часть: iy = Jm z.

Запись комплексного числа в виде z = x + iy называют алгебраической формойкомплексного числа.

Комплексное число равно 0 тогда и только тогда, когда x = 0 и y = 0:

z = x + iy = 0 Û .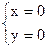

Два комплексных числа равны между собой тогда и только тогда, когда равны их вещественные и мнимые части:

z₁ = x₁+ iy₁, z₂ = x₂ + iy₂,

z₁ = z₂ Û .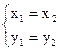

Два комплексных числа, отличающиеся только знаком мнимой части, называются сопряжённымиz = x + iy, z^* = x – iy.

Если z = x+i0, то z – действительное число. Отсюда следует, что действительные числа являются подмножеством комплексных чисел.

Комплексные числа изображаются точками числовой плоскости. Каждому комплексному числу x + iy ставится в соответствии точка M (x, y) координатной плоскости так, что абсцисса точки равна действительной части комплексного числа, а ордината – мнимой части. Координатная плоскость XOY называется при этом комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней расположены точки, соответствующие комплексным числам x + i0, т.е. действительным числам. Ось ординат называется мнимой осью, так как на ней лежат точки, соответствующие чисто мнимым комплексным числам 0 +iy.

Важной и удобной является интерпретация комплексного числа x + iy как вектора 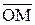, т.е. вектора, исходящего из начала координат 0 (0, 0) идущего в точку M (x, y). Таким образом, устанавливается взаимно однозначное соответствие между комплексными числами и векторами плоскости, выходящими из начала координат.

Для контроля усвоения задать вопрос:Представить графические изображения комплексных чисел: –2-i3 и –2+i3; сделать сравнительный вывод о расположении чисел на комплексной плоскости.

Выводы:Комплексное число в алгебраической форме записи содержит действительную и мнимую части. Комплексное число может изображаться точкой или вектором на комплексной плоскости, координатами которых являются действительная часть и коэффициент при мнимой части комплексного числа.