Тригонометрическая форма комплексного числа.

Построим на комплексной плоскости число z = x + iy и вектор, соответствующий этому числу.

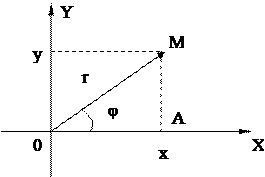(.) M (x, y) Þ z = x + iy;

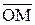Þ z = x + iy.

Определим полярные координаты точки M (j, r), считая точку 0 полюсом, а положительное направление оси OX – полярной осью.

OM = r; Ð MOA = j, тогда из D MOA имеем: x = r × cos j, y = r × sin j.

Тогда комплексное число z = x + iy можно записать в виде z = r cos j + ir sin j или z = r (cos j + i sin j).

Запись комплексного числа в виде z = r (cos j + i sin j) называется тригонометрической формой комплексного числа.

Из D MOA можно найти, r = 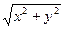, а tg j = 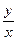или j = arctg .

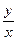Определение. 1.Модулем комплексного числа называется длина вектора, соответствующего этому числу 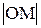= r; r = 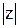; r = ; .

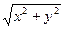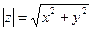Определение. 2.Аргументом комплексного числа называется величина угла между положительным направлением действительной оси и вектором, соответствующим этому числу.

Arg z = Arg (x + iy); Arg z = arc tg .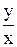

Под Arg z понимается общее значение аргумента, а главное значение arg z берётся в интервале -180⁰ < arg z £ 180⁰.

На практике под аргументом комплексного числа понимается именно главное его значение.

Для контроля усвоения задать вопрос: Записать число z = 1 – i в тригонометрической форме. Ответ: 1 – i = 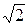(cos 45⁰-isin45⁰).

Выводы: Для представления комплексного числа в тригонометрической форме записи необходимо знание модуля и аргумента комплексного числа. Аргумент комплексного числа принято записывать в пределах от -180^о до +180^o].