Несжимаемой жидкости по закону Дарси

Фильтрационный поток называется радиально-сферическим, если векторы скорости фильтрации направлены в пространстве по прямым, радиально сходящимся к одной точке (или расходящимся от нее).

Благодаря центральной симметрии давление и скорость фильтрации зависят и этом случае только от одной координаты, отсчитываемой от центра (рис. 4.6). Частным случаем потока, весьма близкого радиально-сферическому, является приток жидкости к гидродинамически несовершенной скважине малого диаметра, едва вскрывшей непроницаемую горизонтальную кровлю однородного пласта большой мощности (теоретически бесконечной).

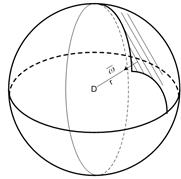
Рис. 4.6. Расчетная схема при радиально-сферическом движении

Пусть на забое скважины, представленной в виде полусфер радиуса r_c, поддерживается постоянное приведенное давление, а на достаточно большом расстоянии от скважины, на полусферической поверхности радиуса R_K сохраняется постоянное давление 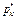и фильтрация в однородном пласте происходит по закону Дарси, то объемный дебит скважины определяется по формуле

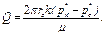(4.35)

Приведенное давление в любой точке пласта определяется по формуле

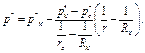(4.36)

а закон движения частиц вдоль линии тока от точки с координатой 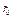до точки с координатой 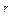описывается уравнением

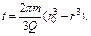(4.37)