Общие сведения об интерполировании

Первоначально под интерполированием понималось отыскание значений функции, соответствующих промежуточным значениям аргумента, которых нет в таблице. При этом интерполяцию можно было бы определить как «искусство чтения между строк». В настоящее время задача интерполяции понимается шире. В известном смысле можно сказать, что задача интерполирования обратна задаче табулирования функции. При табулировании по аналитическому выражению функции находят таблицу ее значений, а при интерполировании, наоборот, по таблице значений функции строят ее аналитическое выражение. Поясним, что следует под этим понимать.

Пусть у= f(x) – некоторая функция, для которой известна лишь таблица ее значений. То есть это значит, что при значениях аргумента х=x₀, x₁,...x_n функция принимает соответственно значения у₀, у₁,...у_n, или, иначе,

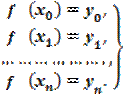(3.1)

Геометрически задача отыскания функции f(x) по заданным ее частным значениям состоит в том, что мы должны построить кривую, проходящую через точки плоскости с координатами (х₀, у₀), (х₁,у₁),...,(х_n,у_n) –рис. 3.1.

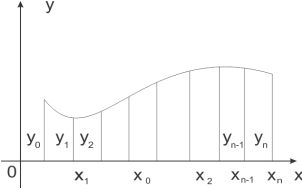
Рис. 3.1

Очевидно, что через данные точки можно провести бесчисленное множество различных кривых. Поэтому задача отыскания функции f(x) по конечному числу заданных ее значений слишком неопределенна. Мы будем обозначать в дальнейшем такую функцию F(х), и их может быть сколько угодно.

Предположим теперь, что функция F(x) не произвольная, а удовлетворяет некоторым дополнительным требованиям, чтобы задача приобретала более определенный характер. Чаще всего требуют, чтобы функция F(x) была многочленом степени, на единицу меньшей, чем число известных значений.

Таким образом, мы приходим к следующей формулировке задачи: для данных значений х = х₀, х₁,..., х_п и у = у₀, у₁ ,...,у_п найти многочлен у = F(x) степени n, удовлетворяющий условиям

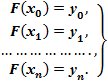(3.2)

Иначе говоря, необходимо отыскать многочлен, принимающий в заданных точках заданные значения. Такую задачу называют задачей параболической интерполяции. Точки х₀, х₁ ,...,х_п называют узлами интерполяции.

Многочлен F(x), удовлетворяющий условиям (3.2), называется интерполяционным, а формулы для его построения – интерполяционными формулами.

Основная идея применения интерполяционных формул состоит в том, что функция у = f(x), для которой известна лишь таблица значений (3.1), заменяется интерполяционным многочленом, который рассматривается как приближенное аналитическое выражение для функции f(x). При этом возникают вопросы о степени точности такого приближения и об оценках погрешности, появляющиеся при замене f(x) наF(x).