Конечные разности
До сих пор мы не делали никаких предположений о значениях аргумента. Предположим, что рассматриваемые значения аргумента являются равноотстоящими. Такое предположение обычно имеет место при интерполировании функций, заданных в виде таблиц с постоянным шагом, т. е.x1 = x0 + h, х2 = х0 + 2h, ..., xm = х0 + mh, гдеh - это шаг таблицы. Построение интерполяционной формулы в этом случае упростится.
Но прежде чем перейти к рассмотрению данного вопроса, необходимо познакомиться с понятием конечных разностей.
Пусть значения функции заданы в точках x0, xn= x0 + h, …, xn = x0 + nh.
Составим разности значений функции:
y1 – y0 = f(x0 + h) – f(x0) = Δy0 = Δf(x0),
y2 – y1 = f(x0 + 2h) – f(x0 + h) = Δy1 = Δf(x0 + h),
……………………………………………………
yn – yn-1 = f(x0 + nh) – f(x0 + (n – 1)h) = Δyn-1 = Δf(x0 + (n – 1)h).
Эти значения называют первыми разностями функции, или разностями первого порядка. По ним мы можем составить разности второго порядка или вторые разности:
Δ2y0 = Δy1 – Δy0, Δ2y1 = Δy2 – Δy1, …, Δ2ym = Δym+1 – Δym.
Разности любого порядка k будут иметь вид
Δkym = Δk-1 ym+1 – Δk-1 ym (3.7)
Эти последовательные разности обычно располагают в форме таблиц. Применяются две формы таблиц последовательных разностей – диагональные и горизонтальные. В диагональных таблицах (табл. 3.1) разности в каждом столбце записываются между соответствующими значениями уменьшаемого и вычитаемого.
Таблица 3.1
| x | y | Разности | |||
| Первые | Вторые | Третьи | ... | ||
| х0 х1 = х0 +h х2 = х0 +2h х3 = х0 +3h х4 = х0 +4h х5 = х0 +5h ….. | у0 у1 у2 у3 у4 у5 ….. | Δу0 Δу1 Δу2 Δу3 Δу4 | Δ2 у0 Δ2 у1 Δ2 у2 Δ2 у3 | Δ3 у0 Δ3 у1 Δ3 у2 |
Так как разности обычно бывают невелики, то их записывают без нулей впереди.
Равенства:(3.7) определяют разности различных порядков последовательно. Интерес представляют выражения для конечных последовательностей, установленные непосредственно через значения функций. Установимих.
Так как
Δy0 = y1 – y0; Δy1 = y2 – y1,
то
Δ2y0 = Δy1 – Δy0 = (у2 – у1) – (у1 – у0).
Поэтому Δ2y0 = y2 – 2y1 + y0.
Точно так же найдем третью разность, выраженную через значения функций:
Δ3y0 = Δ2 y1 – Δ2 y0 = Δy2 – Δy1 – Δy1 + Δy0 =
= (у3 – у2) – 2(у2 – у1) + (у1 – у0) = у3 – 3у2 + 3у1 – у0.
Нетрудно показать, что для любого значения k разность будет иметь
Δky0 = yk – kyk-1 +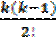 
yk-2 + … + (-1)k-1ky1 + (-1)ky0(3.8)
Формула (3.8) имеет место и для разности Δkym. Достаточно ко всем номерам значений функций прибавить индекс m.
Дата добавления: 2015-02-03; просмотров: 1245;