Обратная интерполяция и многочлены Чебышева
До сих пор мы рассматривали лишь задачи отыскания значений функций, соответствующих данным значениям аргумента, отсутствующим в таблице. Между тем нередко приходится сталкиваться с задачами иного характера: по таблице функции отыскать значение аргументаx, которому соответствует данное значение функции, отсутствующее в таблице. Так поставленную задачу называют задачей обратной интерполяции.
Задачу обратной интерполяции легко обратить, считая значения функции значениями аргумента. Однако так как разности функции отличаются не на постоянную величину, то обратная интерполяция приводит к необходимости интерполировать в таблице, значения аргумента в которой не являются равноотстоящими. По этой причине для обратной интерполяции применяется обычно интерполяционная формула Лагранжа или другие методы.
Пример. Функция у= f(x) задана табл. 3.7, определить, какому значению х соответствует значение функцииу=2,4142.
Таблица 3.7
| х | 0,880 | 0,881 | 0,882 | 0,883 |
| у = f(x) | 2,4109 | 2,4133 | 2,4157 | 2,41181 |
| Чтобы не менять обозначений в интерполяционных формулах, поменяем местами х и у. Тогда будем иметь функцию у = φ(x), значения которой заданы табл. 3.8 и для которой требуется найти φ(2,4142). При этом значения х уже не будут равноотстоящими. |
Таблица 3.8
| х | 2,4109 | 2,4133 | 2,4157 | 2,41181 |
| у = φ(x) | 0,880 | 0,881 | 0,882 | 0,883 |
Пользуясь формулой Лагранжа (3.6), в которой следует положить x==2,4142, найдем

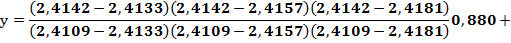
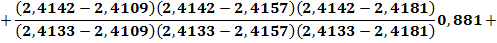
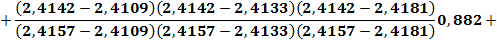
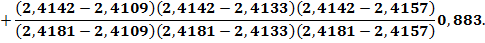
Вычислив значения дробей, получим у = 0,88138.
Таким образом,φ(2,4142) = 0,88138, т.е. значение х, при которойзаданная табл. 3.7 функция f(x), принимает значение 2,4142, равно 0,88138.
При интерполяции на отрезке [а, b] возникает вопрос, как выбрать узлы х0, х1, ..., хn интерполяционного многочлена, чтобы максимальная погрешность интерполяции функцииf(x) была минимальной. Эта задача в общем случае является сложной, и ее удается решить только для частной функции f(x). При этом рассматриваются многочлены Чебышева Тп(х) на стандартном отрезке [-1,1], n ≥ 0. Они задаются формулой
Тn(х) = cos (n · arcos x)(3.15)
В частности, при n = 0,1 имеем
Т0(х) =cos(0 · arcos x) = 1;
Т1(х) = cos(arcos x) = x;
Тn+1(х) = 2xTn(x) - Tn-1(x),(3.16)
где n = 1,2,…
Полагая T0(x) = 1, T1(х) = х на всей оси и распространяя рекуррентную формулу (3.16) на всю ось x последовательно по формуле (3.16) находим
Т2(х) = 2х2 -1, Т3(x)= 4х3-3х,
Т4(х) = 8х4 -8х2+1, Т5(x)= 16х5-5х3+5х,...
Доказано, что узлы, минимизирующие оценку погрешности интерполяции на отрезке [-1,1]многочленом Тn+1(х),определяются соотношением
xi = cos 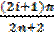 , i = 0,1,2,…, n.
, i = 0,1,2,…, n.
Дата добавления: 2015-02-03; просмотров: 3371;
