Аппроксимация и сплайн-интерполяция функций при автоматизированном проектировании дорог.

Аппроксимация (от лат. approximo - приближаюсь), замена одних математических объектов (напр., чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными).Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). Задача аппроксимации (приближенного представления) возникает при замене кривой или поверхности, описываемых сложными функциями, другими функциями, имеющими более простые уравнения, без потери необходимой точности (моделируемая кривая не обязательно проходит через данные точки, но удовлетворяет некоторому заданному свойству относительно этих точек. Аппроксимация используется например в математическом моделировании рельефа, для упрощения подсчетов в табличных данных и уменьшения времени подсчетов.

Сплайн-интерполяция:

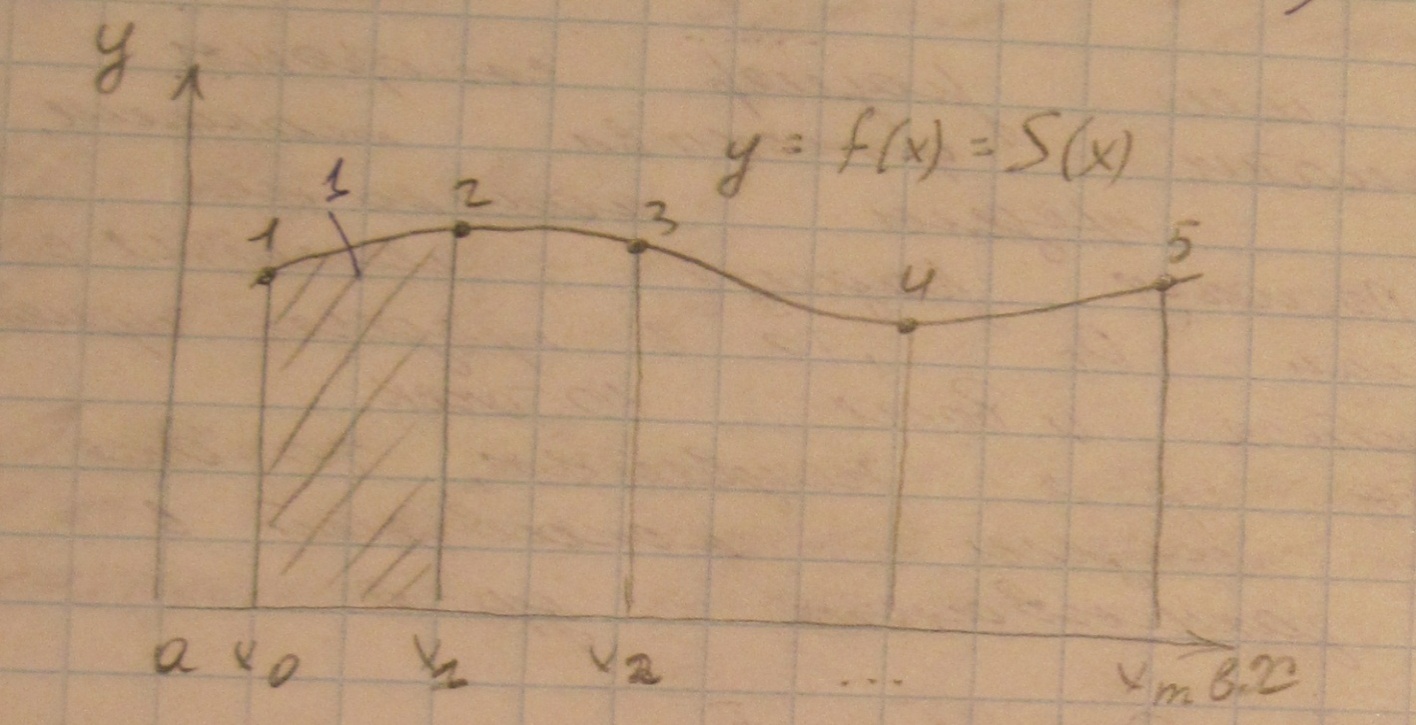
Интерполяция при помощи сплайнов называется сплайн-интерполяцией. Задача интерполяции (приближенного восстановления) связана с поиском гладких кривых или поверхностей, проходящих через множество заданных точек.

Сплайном называется кусочно-полиномиальная система, определенная на отрезке а; в и имеющая на этом отрезке, некоторое количество непрерывных производных.

Преимущества интерполяции сплайнами по сравнению с обычными методами интерполяции заключается в восходимости и устойчивости процесса.