Методы одномерной и многомерной оптимизации в автоматизированном проектировании.

Проектирование автомобильных дорог ведется при жестких ограничениях на разнообразные ресурсы: финансовые, материальные, энергетические, временные. Развитие систем автоматизации проектирования привело к широкому использованию методов оптимизации проектных решений. Реализация этих методов затруднена при ручной технологии проектирования. В САПР быстро находится окончательный, оптимальный вариант проектного решения, эффективно выполняется конструктивное проектирование. При направленном поиске оптимального решения многократно используются процедуры параметрического синтеза.

В общем виде задача оптимизации с ограничениями формулируется следующим образом: найти экстремум (максимум или минимум) функции f(x) при заданных ограничениях

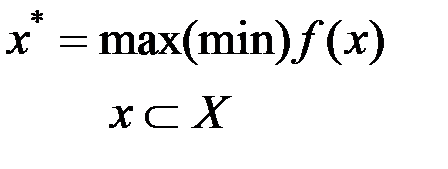, (1.4)

где Х (х1,х2,х3) - подмножество в n-мерном пространстве, f(x) - функция цели (целевая функция).

В основе процессов оптимизации лежит целевая функция, которая формируется с учетом выходных параметров и количественно выражает качество проектируемого объекта.

В САПР-АД сложность выбора целевой функции обусловлена тем, что задача проектирования автомобильных дорог многокритериальная и многие выходные параметры противоречат друг другу. Улучшение одного из выходных параметров, как правило, ведет к ухудшению другого, все они зависят от внутренних параметров и не могут изменяться независимо друг от друга.

Например, повышение безопасности движения и улучшение экологических качеств проектируемой дороги приводят к повышению стоимости строительства. Увеличение расчетной скорости движения не только ведет к увеличению стоимости строительства, но в некоторых случаях приводит к ухудшению экологических показателей и т.д. Для оценки проектных решений необходимо выделить один основной выходной параметр, сведя многокритериальную задачу к однокритериальной. В качестве таких показателей выступают экономические критерии. Очень часто при проектировании автомобильных дорог таким основным параметром считают стоимость строительства или сумму строительных (единовременных) и эксплуатационных (текущих) затрат за определенный период (срок службы дороги).

Определив целевую функцию для оптимизации проектного решения, устанавливают, какие из внутренних параметров не меняются в процессе оптимизации, а по каким будет организован целенаправленный поиск. Для этого внутренние параметры разделяют на постоянные, не подлежащие изменению и переменные - изменяющиеся от варианта к варианту. Именно последние и являются аргументами целевой функции и называются управляемыми параметрами.

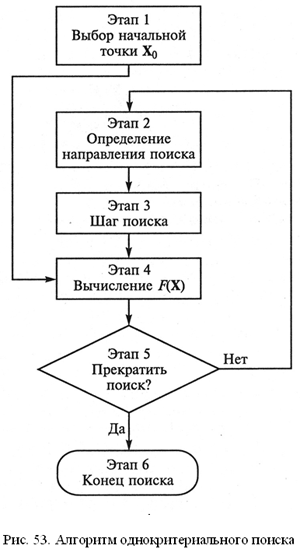
Алгоритм однокритериального поиска оптимального решения представлен на рис. 53

Более сложные многокритериальные методы поиска оптимума, когда оптимизация проводится по нескольким критериям, чаще встречаются в задачах проектирования. В этих случаях алгоритм поиска усложняется. Например, метод Гаусса - Зейделя даже для двух переменных требует уже пространственного представления о протекании функции, по которой находится оптимум. То есть решается задача

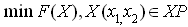
Графическая интерпретация поиска оптимума по этой зависимости представлена на рис. 54.

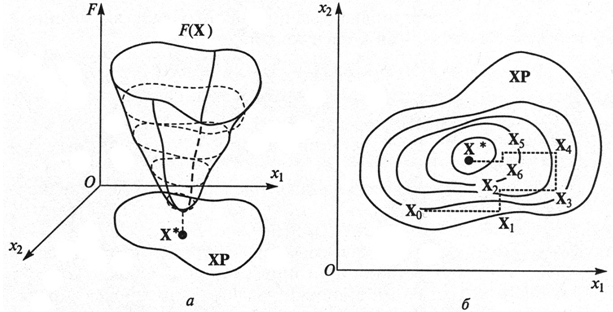
Рис. 54. Принцип оптимизации по двум параметрам

а- поверхность целевой функции, б- проекция функции на плоскость

2.13 «Диагностика автомобильных дорог»