Эмпирические формулы.
Из выше изложенного материала ясно, что любую функцию можно с достаточной степенью точности заменить интерполяционным многочленом. Однако, чтобы добиться достаточно хорошего совпадения, может потребоваться использование многочлена сравнительно высокой степени. Такой многочлен будет неудобен в обращении ввиду его громоздкости, коэффициенты такого многочлена могут и не иметь физического смысла.
Поэтому при проведении натурных экспериментальных исследований или вычислительных экспериментов часто используют другие подходы при установлении неизвестной функциональной зависимости между значениями переменных x и y. Такие зависимости принято называть эмпирическими формулами. Они, как правило, имеют более простой вид, позволяют производить интерполирование и применять к экспериментальным данным методы математического анализа.
Итак, пусть в результате ряда измерений величин x и y получена таблица их значений.
| x | 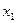
| 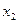
| … | 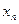
|
| y | 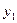
| 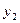
| … | 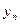
|
Если аналитическое выражение функции f(x) неизвестно или весьма сложно, то возникает практически важная задача: найти эмпирическую формулу
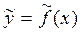 , ,
| (4.1) |
значения которой при 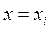 возможно мало отличалось бы от опытных данных
возможно мало отличалось бы от опытных данных 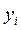 (i=1,2,…,n). В такой постановке наша задача весьма неопределенна. Поэтому обычно указывают достаточно узкий класс функций K (например, линейных, степенных, показательных и т. п.), которому должна принадлежать искомая функция f(x). Дело, таким образом, сведется к нахождению лишь наилучших значений параметров этой функции.
(i=1,2,…,n). В такой постановке наша задача весьма неопределенна. Поэтому обычно указывают достаточно узкий класс функций K (например, линейных, степенных, показательных и т. п.), которому должна принадлежать искомая функция f(x). Дело, таким образом, сведется к нахождению лишь наилучших значений параметров этой функции.
Геометрически задача построения эмпирической формулы состоит в проведении кривой Г вида (1) из некоторого класса К, «возможно ближе» примыкающей к системе точек 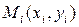 (i = 1,2,…,n), как показано на рисунке 1.
(i = 1,2,…,n), как показано на рисунке 1.
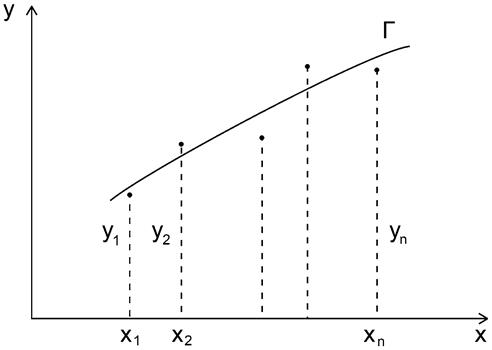
Рис.1
Заметим, что задача построения эмпирической формулы отлична от задачи интерполяции. При интерполировании отыскивается функция из данного класса функций (например, полиномов заданной степени), значения которой в заданных точках  совпадали бы с табличными значениями
совпадали бы с табличными значениями 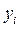 (i = 1,2,…,n). При нахождении эмпирической формулы не требуется, чтобы значения
(i = 1,2,…,n). При нахождении эмпирической формулы не требуется, чтобы значения 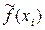 совпадали с
совпадали с 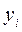 . Достаточно, чтобы разность
. Достаточно, чтобы разность 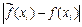 была мала в известном смысле в данной области.
была мала в известном смысле в данной области.
Построение эмпирической формулы слагается из двух этапов.
1) Выяснение общего вида этой формулы;
2) Определение наилучших ее параметров.
Если неизвестен характер зависимости между данными величинами x и y, то предпочтение отдается простым формулам. Нельзя указать общего метода для нахождения наилучшего типа формулы, соответствующей опытным данным.
Удачный выбор эмпирической формулы в значительной мере зависит от опыта и искусства экспериментатора (составителя формулы, – составитель и экспериментатор не всегда могут быть одним и тем же лицом).
В некоторых случаях выбор типа эмпирической формулы может быть произведен на основе теоретических представлений о характере изучаемой зависимости. В других случаях удается подобрать такую формулу, сравнивая кривую, построенную по данным наблюдения, с образцами известных кривых, построенных в декартовых системах координат или в специальных системах координат (полулогарифмической, логарифмической и т. д.). При определенном навыке по положению точек, определяющих некоторую гладкую кривую, можно примерно угадать общий вид зависимости.
Что касается определения наилучших значений параметров, входящих в эмпирическую формулу, то эта задача былее легкая и решается регулярными методами.
При построении эмпирической формулы можно предположить, что исходные данные 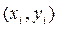 положительны. Действительно, если бы, например, все
положительны. Действительно, если бы, например, все 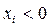 (или все
(или все 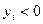 ), то достаточно рассмотреть таблицу значений
), то достаточно рассмотреть таблицу значений 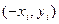 или
или 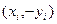 . При
. При 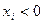 и
и 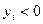 достаточно построить эмпирическую формулу для таблицы
достаточно построить эмпирическую формулу для таблицы 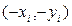 .
.
В общем случае, когда знаки значений 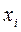 и
и 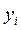 меняется, то всегда можно подобрать положительные числа m и n такие, что
меняется, то всегда можно подобрать положительные числа m и n такие, что
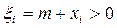 ,
, 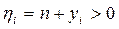 .
.
Отсюда получаем, что решение поставленной задачи сводится к нахождению эмпирической формулы для системы положительных значений 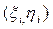 .
.
Дата добавления: 2015-02-03; просмотров: 2360;
