Основные формулы. Кинематическое уравнение движения материальной точки (центра массы твёрдого тела) вдоль оси :

Кинематическое уравнение движения материальной точки (центра массы твёрдого тела) вдоль оси :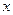

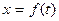
где 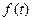–некоторая функция времени.

Проекция средней скорости на ось :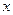

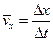
Средняя скорость движения:

=

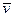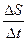
где 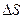- путь, пройденный точкой за интервал времени .

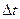Путь 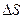, в отличие от разности координат 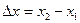, не может убывать и принимать отрицательные значения, т.е. .

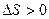Проекция мгновенной скорости на ось :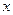

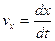
Проекция среднего ускорения на ось :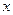

=

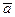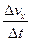
Проекция мгновенного ускорения на ось :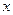

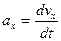
Кинематическое уравнение движения материальной точки по окружности ( ):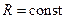

,

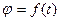Модуль угловой скорости:

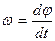
Модуль углового ускорения:

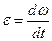
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

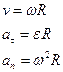
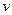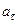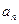где - модуль линейной скорости; и - модули тангенциального и нормального ускорений; 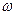– модуль угловой скорости; 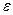- модуль углового ускорения; R- радиус окружности.

Модуль полного ускорения:

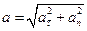или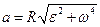

Угол между полным a и нормальным a 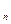ускорениями:

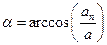
Кинематическое уравнение гармонических колебаний материальной точки:

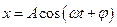
где 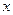- смещение; A– амплитуда колебаний; 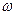- угловая или циклическая частота; 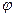-начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

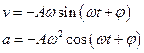
Сложение гармонических колебаний одного направления и одинаковой частоты:

- амплитуда результирующего колебания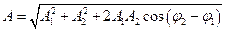

- начальная фаза результирующего колебания

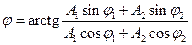
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях:

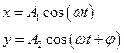
a) 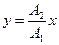если разность фаз ;

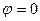б) 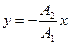если разность фаз ;

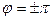в) 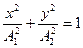если разность фаз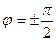

Уравнение плоской бегущей волны:

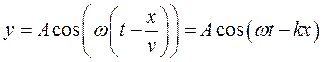
где 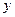- смещение любой из точек среды с координатой 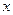в момент 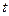; 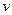- скорость распространения колебаний в среде, 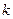– волновое число.

Связь разности фаз 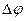колебаний с расстоянием 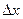между точками среды, отсчитанным в направлении распространения колебаний:

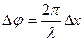
где 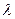- длина волны.

Импульс материальной точки массой m, движущейся со скоростью ,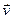

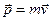
Второй закон Ньютона:

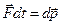
где 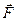- результирующая сила, действующая на материальную точку.