Формул Лагранжа и Ньютона
После построения интерполяционного многочлена возникает вопрос, насколько близко построенный многочлен приближается к функции f(x) в точках, отличных от узлов. В этом случае рассматривают остаточный член
|Rn(x)|=|f(x) – Ln(x)|.
В данном случае Ln(x) – многочлен Лагранжа.
Анализ показывает, что абсолютная погрешность интерполяционной формулы Лагранжа имеет вид
|Rn(x)|=|f(x) – Ln(x) ≤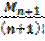 
|Пn+1(x)|(3.17)
где Mn+1 = max |f (n+1)(x)|, f (n+1)(x) – (n+1)-я производная f(x),а
x≤ a≤b
Пn+1(x) = (x – x0) (x – x1)… (x – xn).
Пример. С какойточностью можно вычислить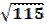 
с помощью интерполяционной формулы Лагранжа второй степени функции у = 
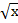, выбрав узлы интерполяции х0 = 100,х1 = 121,х2 = 144
Решение. Вычислим первую, вторую и третью производные функции: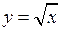 
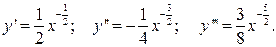
Отсюда очевидно, что максимальное значение М3 будет, если из отрезка [100,144] выбрать x=100, т.е.
M3 = max |y’’’| =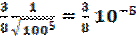 
при 100≤ х ≤144.
На основании формулы (3.17) получаем
|R2| ≤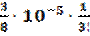 
|(115-100)(115-121)(115-144)| 
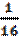·10-5·15·6·29≈1,6·10-3.
Для первой интерполяционной формулы Ньютона (3.11) остаточный член Rn(х) представляется в виде
Rn(х) = h(n+1)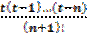 
f(n+1)(ξ) (3.18)
где ξ – некоторое промежуточное значение между узлами интерполирования х0,х1,х2,…, хnи рассматриваемой точкой х;h=xi+1 –xi;t=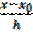 
.
Аналогично получается остаточный член для второй интерполяционной формулы Ньютона (3.13), только здесь t =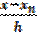 
:
R(x) =hn+1 
f (n+1)(ξ).
Пример. Оценить погрешность приближения функции f(x)=sin xинтерполяционным полиномом пятой степени F5(x),совпадающим с данной функцией при значениях x=00, 50, 100, 150, 200, 250.
Решение. Здесь f (6)(x)= -sin x,поэтому |f(6)(x)| ≤1.На основании формулы (3.18) имеем
|sin x–F5(x)|≤hn+1 |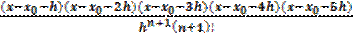 
| <
< 
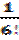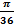|x(x- 
)(x- 
) (x-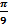 
) (x- 
) (x-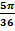 
)|.
Если, например, х=12030’=arc 0,21816,получим
|sin x – F5( x)| < 2,2 · 10-9.
3.7. Разделённые разности
При построении таблицы разностей мы до сих пор предполагали, что значения аргумента функции являются равноотстоящими т.е. имеют постоянный шаг. Однако на практике встречаются таблицы для не равноотстоящих значений аргумента, т.е. таблицы с переменным шагом. Для таких таблиц понятие конечных разностей обобщается в так называемые разделенные разности.
Пусть функция у =f(x) задана таблицей и х0, х1, х2,… – значения аргументов, а у0, у1, у2,… -соответствующие значения функции, где разности Δх1 =хi+1 –xi ≠0,(i=0,1,2,…) не равны между собой.
Отношения
[xi,xi+1] =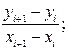 
(i = 0,1,2…)
называются разделенными разностями первого порядка.
Например,
[x0, x1]=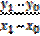 
;[x1, x2]= 
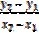;и т.д.
Аналогично определяются разности второго порядка
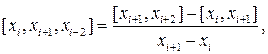(i = 0,1,2,…)
Например, [x0, x1, x2]=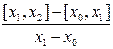 
и т.д.
Вообще разделенные разности n-го порядка получаются из разделенных разностей (n-1)– го порядка с помощью рекуррентного соотношения
[xi ,…, xi+n]= 
;(n = 1,2,…; i = 0,1,2,…).(3.19)
Заметим, что разделенные разности не меняются при перестановке элементов, т.е. представляют собой симметрические функции своих аргументов.
Например, [x0, x1]=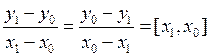 
=[x1, x0]и т.д.
Разделенные разности обычно располагаются в таблице приведенного ниже вида.
Таблица 3.9
| x | y | Разделенные разности | |||
| 1-го порядка | 2-го порядка | 3-го порядка | 4-го порядка | ||
| х0 х1 х2 х3 х4 | y0 y1y2 y3 y4 | [x0, x1] [x1, x2] [x2, x3] [x3, x4] | [x0, x1, x2] [x1, x2, x3] [x2, x3, x4] | [x0, x1, x2, x3] [x1, x2, x3, x4] | [x0, x1, x2, x3, x4] |
Пример. Составить разделенные разности для функции, заданной табл. 3.10
Таблица 3.10
| х | 0,2 | 0,3 | 0,4 | 0,7 | 0,9 | |
| y | 132,651 | 148,877 | 157,764 | 166,375 | 195,112 | 216,000 |
Решение. Последовательно применяя формулу (3.19), получим.
;
;
;
;
;
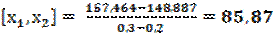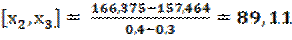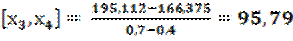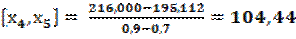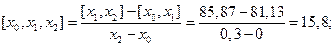
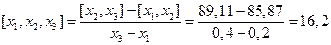
и т.д.
Полностью результаты вычисления приведены в табл. 3.11
Таблица 3.11
| x | y | Разделенные разности | |||
| 1-го порядка | 2-го порядка | 3-го порядка | 4-го порядка | ||
| 0,2 0,3 0,4 0,7 0,9 | 132,651 148,877 157,764 766,375 195,112 216,000 | 81,13 85,87 89,11 94,79 104,44 | 15,8 16,2 16,7 17,3 |
Без подробных выкладок приведем интерполяционную формулу Ньютона для неравноотстоящих значений аргумента
Р(х) = y0 + [x0, x1](x-x0) + [x0, x1, x2](x- x0)(x- x1) + …
…+ [x0, x1, …, xn] (x- x0)(x- x1)…(x – xn-1). (3.20)
Погрешность этой формулы определяется, как обычно, выражением (3.17):
|R(x)| = |f(x) – P(x)| =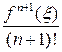 
(x-x0)(x-x1)…(x-xn-1)|,
где ξ – промежуточное значение между точками х0, х1, х2,..., хnих.
Пример. Составить интерполяционный полином для функции y = f(x), заданной табл. 3.12.
Таблица 3.12
| x | 2,5069 | 5,0154 | 7,5270 | |
| y | 0,3989423 | 0,3988169 | 0,3984408 | 0,3978138 |
С помощью этого полинома найти f(3,7608)
Решение. Строим табл. 3.13 разделенных разностей функции y = f(x)
Таблица 3.13
| x | y | 1-й порядок | 2-й порядок | 3-й порядок |
| 2,5069 5,0154 7,5270 | 0,3989423 0,3988169 0,3984408 0,3978138 | -500 -1499 -2496 | -199 -199 |
Используя формулу (3.20), находим:
y=0,3989423 –0,0000500х–0,0000199х(х – 2,5069).
Отсюда получаем
y (3,7608) = 0,3989423 – 0,00005·3,7608 – 0,000019·3,7608 
(3,7608 – 2,5089) = 0,3986604.
Дата добавления: 2015-02-03; просмотров: 1506;