Интерполяционные формулы Ньютона
При получении интерполяционных формул Ньютона, которые используются для тех же целей, что и формула Лагранжа, сделаем дополнительное предположение, что рассматриваются равноотстоящие значения аргумента. Итак, пусть значения функции у = f(x) заданы для равноотстоящих значений x0, x1 = x0 + h, …, xn = x0 + nh. Этим значениям аргументов будут соответствоватьзначенияфункции: у0 = f(x0),у1 = f(x1), …, yn = f(xn).
Запишем искомый многочлен в виде
F(x) = a0 + a1(x - x0) + a2(x - x0)(x - x1) + a3(x - x0)( x- x1)(x - x2) + …
…+ an(x - x0)( x - x1)…(x - xn-1) (3.9)
Для определения коэффициентов a0, a1,..., аn положим в (3.9) х = х0. Тогда у0 = F(x0)=а0. Далее, полагая x=x1, получим у1= F(x1) = a0 + а1h, откуда
a1 =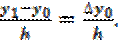 
Продолжая вычисления коэффициентов, положим х = х2. Тогда
y2 = y0 + 
2h + a22hh, y2 – 2Δy0 = a22h2;
y2 – 2y1 + 2y0 – y0 = y2 – 2y1 + y0 = a22h2.
Исходя из (3.8), получаем y2 – 2y1 + y0 = Δ2y0.
Поэтому
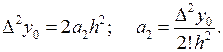
Точно так же получим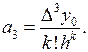 
Аналогичные дальнейшие вычисления позволяют записать общую формулу для любого коэффициента аk:
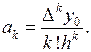
Подставим найденные выражения коэффициентов в формулу (3.9), получим
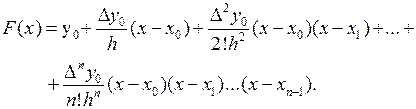(3.10)
Полученная формула и называется первой интерполяционной формулой Ньютона.
Для практического использования формулу Ньютона (3.10) обычно записывают в преобразованном виде. Для этого введем обозначение
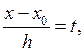отсюда х = х0 + ht.
Выразим через t множители, входящие в формулу (3.10):
………………………..
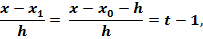
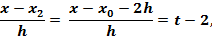
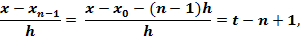
Подставив полученные выражения в формулу (3.10), окончательно получаем
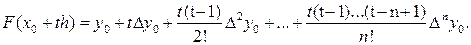(3.11)
Выражение (3.11) представляет окончательный вид первой интерполяционной формулы Ньютона.
Пример. Приняв шаг h =0,05,построить на отрезке [3,5; 3,7] интерполяционный полином Ньютона для функции y = ex,заданной табл. 3.3.
Таблица 3.3
| x | 3,50 | 3,55 | 3,60 | 3,65 | 3,70 |
| y | 33,115 | 34,813 | 36,598 | 38,475 | 40,447 |
Решение. Составим таблицу разностей
Таблица 3.4
| х | y | Δy | Δ2y | Δ3y |
| 3,50 3,55 3,60 3,65 3,70 | 33,115 34,813 36,598 38,475 40,447 |
Заметим, что в столбцах разностей, следуя обычной практике, мы не отделяем запятой десятичные разряды, которые ясны из столбца значений функций.
Так как разности третьего порядка практически постоянны, то в формуле (3.11) полагаем n = 3.Приняв х0 = 3,50и у0 = 33,115,будем иметь:
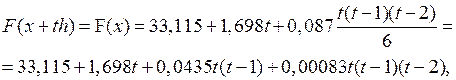
где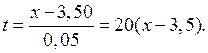 
Первая интерполяционная формула Ньютона неудобна для интерполирования функции в конце таблицы, где число значений разностей мало. В этом случае применяется вторая интерполяционная формула Ньютона, которую мы сейчас и рассмотрим.
Напишем искомый интерполяционный многочлен в виде
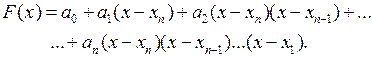(3.12)
Как и ранее, коэффициенты а0,а1,…аnопределяются из условия F(xi) = yi.Положим в (3.12) х = хn.Тогда a0 = yn.
Точно так же, полагая x = xn-1, получим yn-1 = yn +a1(xn-1 - xn),
а так как xn-1 – xn = - h,то
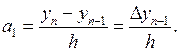
Далее, полагая в (3.12) x = xn-2и, заменяя найденные коэффициенты а0, а1их значениями, получаем
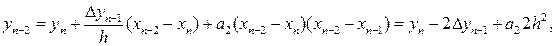
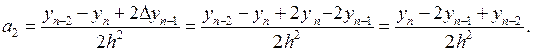
Числитель последнего выражения можно представить так:
yn –yn-1 – (yn-1 -yn-2)=Δyn-1 -Δyn-2 =Δ2yn-2.
Поэтому
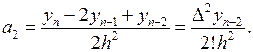
Продолжая аналогичные вычисления, получим общую формулу для коэффициентов
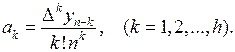
После подстановки в (3.12) всех значений коэффициентов эта формула примет вид
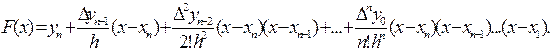(3.13)
Это и есть вторая интерполяционная формула Ньютона. Для удобства применения ее, как и первую, преобразуют, введя обозначения
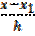= tили x=xn +th.
Выразим теперь через t множители в формуле (3.13):
……………………………………………..
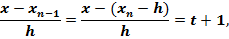
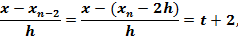
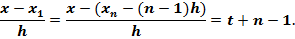
Произведя такую замену, окончательно получим:
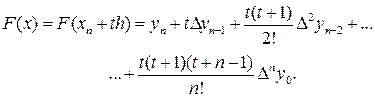(3.14)
Пример. По табл. 3.5 значений семизначных логарифмов для чисел от 1000 с шагом 10 найти lg 1044.
Таблица 3.5
| x | y | Δy | Δ2y | Δ3y |
| 3,0000000 3,0043214 3,0086002 3,0128372 3,0170333 3,0211893 | -426 -418 -409 -401 |
Примем xn =1050,yn =3,0211893;Δyn-1 =0,0041560;
Δ2yn-2 = -0,0000401;Δ3yn-3=0,0000008.Тогда для x=1044 получаем
t =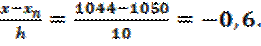 
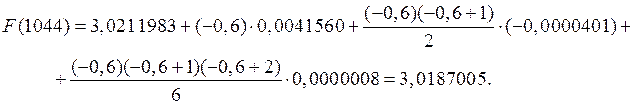
Как первая, так и вторая интерполяционные формул Ньютона могут быть использованы для экстраполирования функций, т. е. для нахождения значений функций для значений аргументов х, лежащих вне пределов таблицы. Еслизначение x<x0 и значение x близко к x0, то выгодно применять первую интерполяционную формулу Ньютона, причем
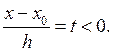
Еслиже x > x0 и x близко кхп, то удобнее пользоваться второй интерполяционной формулой Ньютона, причем
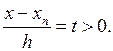
Таким образом, первая интерполяционная формула Ньютона обычно используется для интерполирования вперед и экстраполирования назад, а вторая интерполяционная формула Ньютона, наоборот, – используется для интерполирования назад и экстраполирования вперед.
Пример. Имея табл. 3.6 значений и разностей,у=sin х: в пределах отх=15° дох = 55° с шагом h =5°, найти sin 14° и sin 56°.
Таблица 3.6
| x(0C) | y | Δy | Δ2y | Δ3y |
| 0,2588 0,3420 0,4226 0,5000 0,5736 0,6428 0,7071 0,7660 0,8192 | 832 532 | -26 -32 -38 -44 -49 -54 -57 | -6 -6 -6 -5 -5 -3 |
Решение. Для вычисления sin140 примем x0 =150 и x=140,отсюда t =(14–15)/5 = – 0,2.
Здесь следует выполнить экстраполирование назад, поэтому применим первую интерполяционную формулу Ньютона и подчеркнутые одной чертой конечные разности:
sin140 =0,2588 + (– 0,2)0,0832+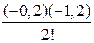 
(– 0,0026) +
+ 
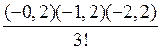(–0,0006) =0,242.
Для отыскания sin560 примем xn =550 и x=560,отсюда t=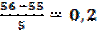 
.
Применяя вторую интерполяционную формулу Ньютона (3.14) и, используя дважды подчеркнутые разности, будем иметь:
sin560 =0,8192+0,2·0,0532+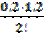 
(-0,0057)+ 
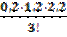(-0,0003)=0,83.
Дата добавления: 2015-02-03; просмотров: 8601;