Второй закон Ньютона

В рассматриваемых ниже физических задачах фундаментальную роль играет второй закон Ньютона. Он гласит, что ускорение, с которым движется тело, прямо пропорционально действующей на него силе (если их несколько, то равнодействующей, т.е. векторной сумме сил) и обратно пропорционально его массе: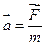

В ситуации, когда сила или масса не являются величинами постоянными, необходимо записать этот закон в более общей математической форме.

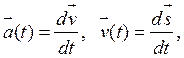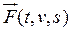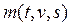Допустим, что сила или масса (или и то, и другое) непостоянны и заданным образом зависят от времени, скорости движения или перемещения: и . Достаточно хотя бы одной зависимости, чтобы ускорение было величиной переменной. Тогда формула Ньютона определяет значение ускорения в тот момент времени, которому соответствуют сила и масса. Интерес представляет временная зависимость перемещения 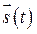и скорости 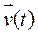Поскольку ускорение есть приращение скорости, а скорость — приращение перемещения, то

(1)

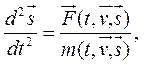а сам второй закон Ньютона приобретает вид

(2)

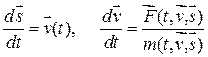или, что то же самое,

(3)

Произведем дискретизацию по времени. Пусть в начальный момент времени t₀ величина s имеет значение s₀ а величина v – значение v₀. Тогда в некоторый последующий момент времени 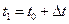будем иметь

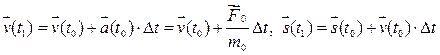(4)

В последующие моменты времени можно поступать аналогично (4). Так, если известны значения v_i, и s_i в момент t_i , то

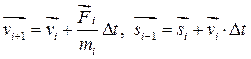(5)