Построение графика.
Выделим диапазон ячеек B3:B20, содержащий данные для построения графика. Значения из столбца A (диапазон A3:A20) будут откладываться по оси ОХ (ось времени), значения из столбца B (диапазон B3:B20) – по оси OY.
Выберем команду Вставка, Диаграмма. С помощью мастера диаграмм построим график в четыре этапа (шага):
Шаг 1.
В диалоговом окне Тип диаграммы на вкладке Стандартные выбрать тип диаграммы Точечная и вид– Точечная диаграмма со значениями, соединенными сглаживающими линиями.
Щелкнуть на кнопке Далее.
Шаг 2.
В окне Источник данных диаграммы на вкладке Диапазон данных проверить, что диапазон данных выбран правильно и установлен флажок опции Ряды в столбцах.
Выбрать вкладку Ряд и в поле Имя: ввести название графика Зависимость v от t.
Установить курсор в поле «Подписи оси Х» и занести диапазон ячеек по переменной t (столбец А – диапазон A3:A20).
Щелкнуть на кнопке Далее.
Шаг 3.
На этом шаге задаются параметры диаграммы (окно Параметры диаграммы).
На вкладке Заголовки ввести название диаграммы и наименования осей координат с указанием единиц измерения величин, откладываемых по этим осям:
в поле Название диаграммы — График зависимости v от t;
в поле Ось X (категорий) — Время t, (с);
в поле Ось Y (значений) — Скорость v, (м/c).
Шаг 4.
Последний шаг определяет местоположение диаграммы – окно Размещение диаграммы.Выбрать вариант –на том же листе.
Щелкнуть на кнопке Готово.
Результаты вычислений, выполненных в табличном процессоре:

Рисунок 1
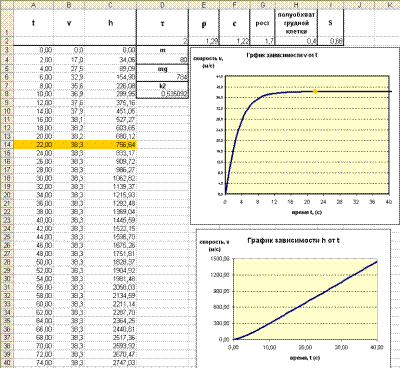
Рисунок 2
Учтем, что t для разных задач нужно выбирать индивидуально. Если в задаче о безпарашютисте можно t взять равным 2 сек., то в задаче о парашютисте (при k2 @ 20) t равно 0,2 сек, т.к. скорость падения меньше. При падении в вязкой среде скорость чрезвычайно мала, поэтому t берется очень маленьким – например, 0,01 – 0,02 сек. При падении в вязкой среде нужно учитывать линейную составляющую скорости в силе сопротивления.
Примерно через 22 сек. после начала полета скорость становится постоянной и остается такой до приземления. Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости заменился бы касательной к нему в начале координат.
Задача о падении шарика в вязкой среде
Шар, сделанный из чугуна, радиуса r = 0,1 м падает в глицерине, встречая силу сопротивления, пропорциональную скорости и силу гидростатического выталкивания (силу Архимеда). Найти изменение скорости и высоты падения при изменении времени. Построить графики зависимости скорости и высоты от времени.
Решение.
На шарик, падающий в вязкой среде, по вертикали действуют три силы:
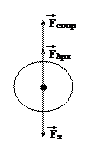
- сила тяжести (тяготения) 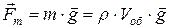 где Vоб – объем шара;
где Vоб – объем шара;
- сила гидростатического выталкивания (сила Архимеда): 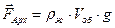
где 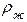 – плотность жидкости,
– плотность жидкости,
- сила сопротивления среды: 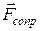 .
.
Учитывая действие трех сил, аналогично системе (7) в проекции на вертикальную ось в данном случае получим:
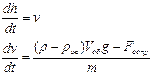 (16)
(16)
Докажем, что скорость мала и квадратичную составляющую скорости в Fcoпp можно не учитывать. При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение Fcoпp = k1v, где k1 определяется свойствами среды и формой тела. Например, для шарика k1 = 6πμr - это формула Стокса, где r - радиус шарика, μ -динамическая вязкость среды.
Таблица вязкости текучих веществ при t = 20°С и давлении 1 атм
| Вещество | μ , [Н∙с/м2] |
| Воздух | 0,0182 |
| Вода | 1,002 |
| Глицерин |
Оценим, при какой скорости для падающего вертикально шара силы сопротивления и выталкивания сравняются с силой тяжести и движение станет равномерным, то есть:
Fт= FАрх+ Fcoпp,
Имеем
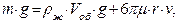
или
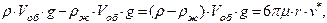
Пусть r = 0,1 м, плотность чугуна: 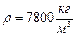 , плотность глицерина:
, плотность глицерина: 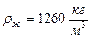 , вязкость глицерина:
, вязкость глицерина: 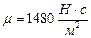 .
.
Учитывая, что 1Н (Ньютон) = 1(кг×∙м)/с2, то вязкость глицерина можно выразить: 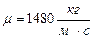 . Тогда:
. Тогда: 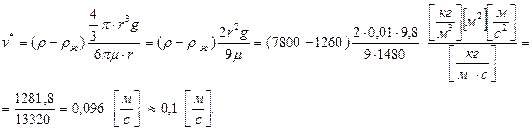
Итак, при падении шара в глицерине скорость, при которой движение станет равномерным, равна v* ≈ 0,1 м/с. Таким образом, скорость достаточно мала, поэтому вкладом квадратичной составляющей силы сопротивления можно пренебречь, то есть действительно Fсопр= k1v. Учитывая обозначение: 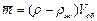 , получим систему уравнений:
, получим систему уравнений:
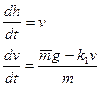 (17)
(17)
Это эквивалентно системе (16), что и требовалось доказать.
В соответствии с методом Эйлера-Коши запишем итерационное уравнение нахождения значения скорости vi+1 через vi. Обозначим правую часть второго уравнения системы (17), записанного в дискретном виде, через 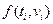 :
:
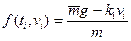 (18)
(18)
Согласно методу Эйлера – Коши запишем формулы:
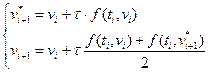 (19)
(19)
Тогда подставляя (18) в формулы (19), получаем

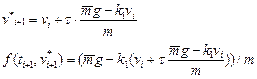
В итоге получим:
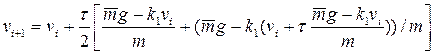 (20)
(20)
Рассмотрим теперь первое уравнение в системе (16), поскольку нам необходимо также исследовать зависимость высоты полета h от времени:
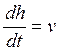
Получим итерационную формулу для вычисления h:

или
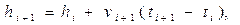
Поскольку 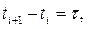
Тогда
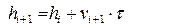 (21)
(21)
Данная задача решается с помощью табличного процессора Excel.
В таблице Excel расположим в столбце D начальные данные:
в D2 – значение τ =0,02,
 в D4 – значение m(
в D4 – значение m( 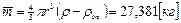 )
)
 в D6 – значение m∙g
в D6 – значение m∙g
в D8 – значение k1 (k1 = 6πμr =2788,32 [Н∙с∙м-1])
в D10 – значение m ( 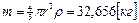 )
)
Тогда для вычисления значения v1 в соответствии с итерационной формулой (20) в столбце В в ячейке В4 нужно записать формулу:
=B3+$D$2/2*(($D$6–$D$8*B3)/$D$10+($D$6–$D$8*(B3+$D$2*($D$6–
–$D$8*B3)/$D$10))/$D$10)
и произвести автозаполнение столбца В.
В столбце С в ячейку С4 нужно записать формулу: = С3+B4*$D$2 в соответствии с итерационной формулой (21) и произвести автозаполнение столбца C.
С использованием итерационных формул таблица имеет вид:

Результаты вычислений, выполненных в табличном процессоре:
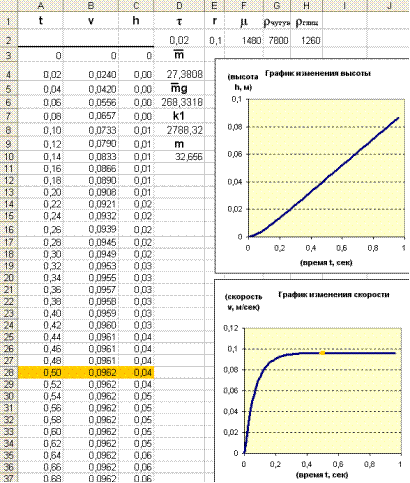
Вывод: примерно через t=0,5 сек. после начала падения скорость становится постоянной и остается такой до конца (график выравнивается, становится параллельным оси изменения времени). При падении в вязкой среде скорость мала, за доли секунды она становится постоянной, поэтому шаг по времени τ берется очень маленьким, например 0,02 сек.
Дата добавления: 2015-01-13; просмотров: 3696;
