ЗАКОНЫ ПОДОБИЯ.

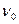Будучи брошенным под углом к горизонту с начальной скоростью , тело летит без учета сопротивления воздуха по параболе и через некоторое время падает на землю.

Решим задачу сначала без учета сопротивления воздуха. Разложим скорость на горизонтальную и вертикальную составляющие:

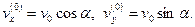(1)

Движение по вертикали не равномерно. Оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным после неё. Движение по горизонтали является равномерным. Для вертикальной составляющий 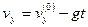; Вычислим время достижения верхней точки траектории. Имеем в верхней точке 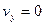, тогда в верхней точке , . Отсюда время достижения верхней точки:

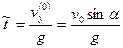(2)

Высота этой точки 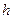равна:

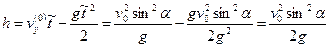(3)

Полное время до падения на землю 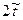; за это время, двигаясь равномерно вдоль оси х со скоростью 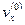, тело пройдет путь:

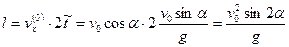(4)

Для нахождения траектории достаточно из текущих значений х и у исключить t:

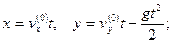(5)

следовательно:

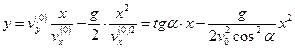(6)

Уравнение (6) – уравнение параболы.

Рассмотрим эту задачу с учетом сопротивления воздуха. При большой начальной скорости полета тела, сопротивление воздуха может значительно изменить движение. Приступим к ранжированию и выясним какой из составляющих силы сопротивления (линейной или квадратичной) можно пренебречь.

Оценку проведем для шарика. (Она не зависит от формы тела). Шарик радиусом r ≈ 0,1 м, движущийся со скоростью 1 м/с, испытывает в воздухе линейную составляющую силы сопротивления 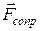(по закону Стокса):

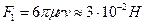
и квадратичную составляющую силы сопротивления

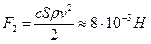
Мы видим, что F₁ и F₂ различаются менее, чем в пять раз. Они одного порядка. Поэтому, если исследуется движение брошенного мяча, то учитываются обе составляющие 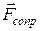. Однако, если моделируется полет снаряда, где скорость – сотни метров в секунду, то линейной составляющей можно пренебречь. Запишем проекции уравнения закона Ньютона 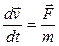на оси х и у, получим:

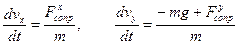(7)

Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то

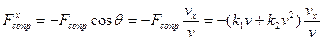
(8)

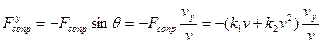
где θ – угол между текущим направлением скорости и осью х. Подставляя (8) в уравнения (7) и учитывая, что 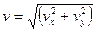, получаем уравнения движения в переменных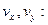

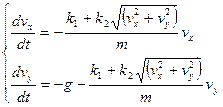(9)

Поскольку представляет несомненный интерес и траектория движения, дополним систему (9) еще двумя уравнениями

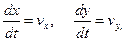(10)

Решая системы (9) и (10) получим четыре функции: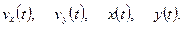

Системы (9) и (10) описывают движение с учетом сопротивления среды.